physiker99
- 36
- 0
This question is about normalizing a wave packet, this is actually the solution and I couldn't understand 2 points.
- I cannot see how the red encircled part do not diverge to infinity.
- And I cannot understand how the very last line is derived from the 2nd last one.
For the second one I tried to call i(po-px) as A and 1/(deltaX) B but that did not lead anywhere.
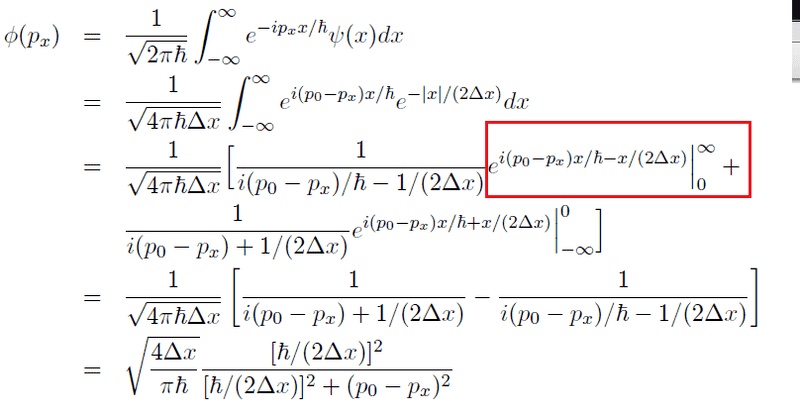
- I cannot see how the red encircled part do not diverge to infinity.
- And I cannot understand how the very last line is derived from the 2nd last one.
For the second one I tried to call i(po-px) as A and 1/(deltaX) B but that did not lead anywhere.