Not-So-Parallel Plate Capacitor

[Enemy0fGods]

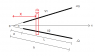
1. You have fabricated a parallel plate capacitor in your work shop, but the square metal plates end up not being exactly parallel to each other. They form an angle $$\alpha$$. The plates, size L, are held at constant electrical potentials, V₁ and V₂, corresponding to an electrical potential difference $$\Delta$$V = V₁ - V₂. Plate 1 holds a +Q charge while plate 2 holds a -Q charge.

I'm done with parts a-c, but I need help with these:

d: Find the total charge carried by the plates (Hint: This requires an integral).
e: Show that the value of the capacitance of this capacitor is C = ($$\epsilon$$₀L)/$$\alpha$$ *ln(b/a). Does this have all the usual attributes of a capacitance?

[PLAIN]http://img19.imageshack.us/img19/220/unledeyr.png

2. Homework Equations : Already listed one, and E=V/d, and the rest I don't know.



3. The Attempt at a Solution : I don't really have an attempt, I'm stuck, all I know is I'm suppose to use an integral with part d, which is already given anyway.

Thanks for any help.

 

[SammyS]

Out of curiosity, what were parts a - c ? & what were your answers to those?

 

[Inna]

2. Homework Equations : Already listed one, and E=V/d, and the rest I don't know.

What do you mean by "d" ? The distance between the plates varies with x.

 

[cupid.callin]

for (e)

consider the part of capacitor inside red rectangle ... it is also a capacitor.
find capacitance of this capacitor in terms of variables you know and x,dx ...
then integrate ...

 

[cupid.callin]

and for d
question itself says plate 1 has charge Q and plate 2 has charge -Q
so total charge would be 0 right?

 

[Idoubt]

and for d
question itself says plate 1 has charge Q and plate 2 has charge -Q
so total charge would be 0 right?

Perhaps the question meant the charge on each plate in terms of potentials and capacitance.

 

[cupid.callin]

but why would question ask that
for (d) first you should do e
so d must be placed next to e ... which it is not