priceofcarrot said:
I'm still confused about the "But that's only because as x gets very large positvely or negatively (x→±∞), y=1/f(x) approaches zero." part though.
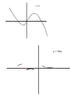
Because to me the reciprocal function in your graph approaches 0 when x becomes a larger negative value, or a smaller negative value. It also distances itself from 0 when x becomes a larger or smaller negative value.
Ignore what's happening for small values of x (such as around the roots of f(x)). When you're looking for horizontal asymptotes you only need to consider what's happening when x gets very large positively (x \to +\infty) or x gets very large negatively (x \to -\infty) and judging by what your graph for f(x) looks like at these values of x, as x\to+\infty, f(x)\to -\infty (does this make sense?) and as x\to-\infty, f(x)\to +\infty.
So what does this mean for your reciprocal function 1/f(x)? Well, since we had that as x\to+\infty, f(x)\to -\infty that means that 1/f(x)\to 0. This means that there is an asymptote of f(x)=0 or y=0.
If we also do the same thing for what happens when x\to -\infty again we'll get that there is an asymptote of f(x)=0.
Now, the reason we can just ignore what happens for smaller values of x (we call this "what happens locally") is because asymptotes can be cut many times. If your function has an asymptote of y=1 for example, even if you let y=1, and you solve for x to find that x=3 for example, it doesn't change the fact that y=1 could still be an asymptote (the value approached but never reached as x gets very large).
priceofcarrot said:
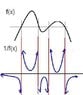
Also, for the initial graph of 1/f(x) that I included, I'm not supposed to use graphing software to draw it. So I have to do it by hand. How do I figure out how far to draw the different parts of the graph?
For the vertical asymptotes, you should draw a dashed line of x=c (c being some constant where the vertical asymptotes occur) and then draw your graph such that it looks obvious that as x gets closer to c, your function 1/f(x) approaches infinite. The way you do this is by drawing your graph relatively vertically next to the asymptote, and when you reach the end of your graph paper or whatever you're drawing on, add an arrow head at the end like so --->
Also, you should add arrow heads onto your graph at the end-points (the largest positive and negative values of x that you can fit), and it should be clear that y=0 is an asymptote because you should draw your graph relatively horizontally near y=0 at these end-points.
Can you figure out how many arrow heads your graph should have then?