- #1
The New Guy
- 10
- 0
Hey there, guys. I’m kind of new to the whole physics thing, but I am starting on a quest to try and learn as much about how this universe works as I can. I am currently working on developing a good understanding of special and general relativity. I am not overly math-competent, so I have been sticking to the conceptual area of relativity as much as I possibly can. I have done quite a bit of studying on the subject, and I have most of the concepts at least “memorized.” I don’t necessarily “understand,” however, so don’t feel too shocked if I say a few things that make you scratch you heads.
In trying to fully comprehend special relativity, the biggest road block I’ve hit is this: I don’t understand where the physical slowing of time for objects in relative motion comes into play in preserving the speed of light in all reference frames. This is what I am hoping you guys can answer for me.
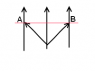
I have seen some examples. The most common one is the “light clock,” a clock where a beam of light bounces back and forth between two panels, and each period is one “tick” of the clock. To an observer who is stationary relative to the light clock, the light bounces back and forth between the panels along the shortest possible path. However, when the clock is put into near-light-speed-motion relative to the observer, the light has to travel a longer, diagonal path between the panels due to the fact that the clock itself has changed position. When in relative motion with its observer, the clock ticks more slowly. I understand this, and it makes perfect sense. However, what I am having trouble understanding is why it has to be that this applies to all things, and not just the light clock. In other words, I don’t understand why an hour glass takes longer than an hour to cycle through when viewed by an observer in relative motion, or why a person can take a high-speed journey for 100 years and come back only 50 years aged.
I know I am wrong here, but it seems to me like relative simultaneity and length contraction would be enough to preserve the speed of light without any time dilation in addition. For example, a person is standing stationary with respect to two lightning rods, one that is 1,000,000 miles to his left, and another that is 1,000,000 miles to his right, and he sees two simultaneous lightning strikes. Meanwhile, I am whizzing past him in a rocket from left to right, traveling at near the speed of light. I fly into the wave of light coming from the lightning strike on the right, and the one from the left has to chase me down from behind. I see the lightning strike that I am flying towards before I see the lightning strike that I am flying away from. Both lightning strikes occurred the same distance from me, and advanced towards me at exactly speed c, and D=RT, so that means that the lightning strike that I was flying towards actually happened first, and the speed of light is preserved. I also understand that there is a length contraction in there, but I won’t go into the details of that. What I don’t see is where each observer viewing the other observer’s clock as running slowly comes into play here. It seems as though the speed of light is already preserved, and the laws of physics are the same in both reference frames, and it is mission accomplished. Where is my thinking off here?
I’m hoping you guys can give me a mental picture of why time dilation has to be, so that I can truly understand this stuff. I understand that it might be impossible without getting mathematically involved, so feel free to just say so if it is.
Thanks a bunch!
In trying to fully comprehend special relativity, the biggest road block I’ve hit is this: I don’t understand where the physical slowing of time for objects in relative motion comes into play in preserving the speed of light in all reference frames. This is what I am hoping you guys can answer for me.
I have seen some examples. The most common one is the “light clock,” a clock where a beam of light bounces back and forth between two panels, and each period is one “tick” of the clock. To an observer who is stationary relative to the light clock, the light bounces back and forth between the panels along the shortest possible path. However, when the clock is put into near-light-speed-motion relative to the observer, the light has to travel a longer, diagonal path between the panels due to the fact that the clock itself has changed position. When in relative motion with its observer, the clock ticks more slowly. I understand this, and it makes perfect sense. However, what I am having trouble understanding is why it has to be that this applies to all things, and not just the light clock. In other words, I don’t understand why an hour glass takes longer than an hour to cycle through when viewed by an observer in relative motion, or why a person can take a high-speed journey for 100 years and come back only 50 years aged.
I know I am wrong here, but it seems to me like relative simultaneity and length contraction would be enough to preserve the speed of light without any time dilation in addition. For example, a person is standing stationary with respect to two lightning rods, one that is 1,000,000 miles to his left, and another that is 1,000,000 miles to his right, and he sees two simultaneous lightning strikes. Meanwhile, I am whizzing past him in a rocket from left to right, traveling at near the speed of light. I fly into the wave of light coming from the lightning strike on the right, and the one from the left has to chase me down from behind. I see the lightning strike that I am flying towards before I see the lightning strike that I am flying away from. Both lightning strikes occurred the same distance from me, and advanced towards me at exactly speed c, and D=RT, so that means that the lightning strike that I was flying towards actually happened first, and the speed of light is preserved. I also understand that there is a length contraction in there, but I won’t go into the details of that. What I don’t see is where each observer viewing the other observer’s clock as running slowly comes into play here. It seems as though the speed of light is already preserved, and the laws of physics are the same in both reference frames, and it is mission accomplished. Where is my thinking off here?
I’m hoping you guys can give me a mental picture of why time dilation has to be, so that I can truly understand this stuff. I understand that it might be impossible without getting mathematically involved, so feel free to just say so if it is.
Thanks a bunch!
Last edited: