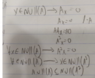sarumman
- 2
- 1
Homework Statement
given
Homework Equations
rank
dim
null space
The Attempt at a Solution
I tried to base my answer based on the fact that null A and null A^2 is Contained in F (n)
and
dim N(A)+rank(A)=N
same goes for A^2.