- #1
nour halawani
- 5
- 0
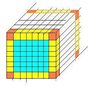
number of atoms in FCC gold cube with only the radius given!
1)it is given that the radius of a gold atom sphere is 144.2 pm, gold is packed in an FCC manner
Give the ratio Ns/Nv as a function of L (gold cube side) and a parameter
of FCC latice, knowing that Ns is the number of surface atoms and Nv is the number of atoms per volume.
2) and 3)
what i am thinking is:
in a unit cell we have 1/8 x 8 corner atoms = 1 atom and in the center of each phase we have 1/2 x 6 = 3 then the total number of atoms will be 4
atoms per unit = 4
volume of the cube is L^3 and volume of the unit is a^3 so if we want to know how many units are there in this cube we can divide the volume of the cube over the volume of the unit cell and we will have L^3/a^3
and if we multiply them by 4 which is the number of atoms per unit we will have the number of atoms in a cubic volume Nv= 4L^3/a^3
now talking about the surface is the thing confusing me
counting the atoms in unit cell is it 2 coming from 4 corners shared by 4 cells which is 1/4 x 4 and 1 center atom and by this we will have 2 atoms or my thinking is not reasonable?
1)it is given that the radius of a gold atom sphere is 144.2 pm, gold is packed in an FCC manner
Give the ratio Ns/Nv as a function of L (gold cube side) and a parameter
of FCC latice, knowing that Ns is the number of surface atoms and Nv is the number of atoms per volume.
2) and 3)
what i am thinking is:
in a unit cell we have 1/8 x 8 corner atoms = 1 atom and in the center of each phase we have 1/2 x 6 = 3 then the total number of atoms will be 4
atoms per unit = 4
volume of the cube is L^3 and volume of the unit is a^3 so if we want to know how many units are there in this cube we can divide the volume of the cube over the volume of the unit cell and we will have L^3/a^3
and if we multiply them by 4 which is the number of atoms per unit we will have the number of atoms in a cubic volume Nv= 4L^3/a^3
now talking about the surface is the thing confusing me
counting the atoms in unit cell is it 2 coming from 4 corners shared by 4 cells which is 1/4 x 4 and 1 center atom and by this we will have 2 atoms or my thinking is not reasonable?