[Number Theory] Finding principal ideals in Z[√-6]

[Firepanda]

[Number Theory] Find all the ideals with the element 6 in them in Z[√-5]

Edited original question since I have now found the answer (I realize the title is inconsistent on the forum page), instead I am now trying to do part i) here

Is it possible to it this way:

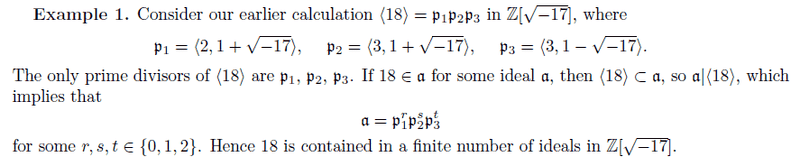
Or is the structure of the question meaning my lecturer wants the actual ideals, and not just a general form? If so, how do i find which ideals contain 6.

I know the general form is

a = p^aq^br^c

Whre a is an element of {0,1,2}, and b,c are an element of {0,1}

So there are 9 different combinations I think, do I have to check all 9? Or do all 9 have this property and there is no need to check?

Thanks

 

[morphism]

Hint: An ideal contains 6 iff it contains (6)=(2)(3) (principal ideals) iff it divides (2)(3).

So factor (2) and (3) in Z[sqrt{-6}].