Muizz
- 11
- 0
I'm working on an assignment where I'm required to numerically find the energy of a delta-potential's bound state. To do this, we've converted the time-independent schrödinger equation to an eigenvalue problem with E the eigen value, ψ the eigen vector and H a matrix as follows:
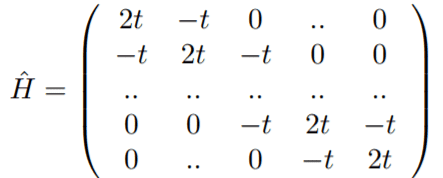
with ##t = \frac{\hbar^2}{2ma^2}##.
Now, my specific problem is this:

I've already done all the theoretical calculations, and am just left with figuring out the code. I've tried a bunch of things, but I haven't been able to get the bound state to appear. My code is as follows:
I'm quite desperate, hence the post here. Thanks in advance for all your help!
For those amongst you who'd prefer a nicely formatted image of the assignment: https://puu.sh/yKp4D/b668471918.png
with ##t = \frac{\hbar^2}{2ma^2}##.
Now, my specific problem is this:
I've already done all the theoretical calculations, and am just left with figuring out the code. I've tried a bunch of things, but I haven't been able to get the bound state to appear. My code is as follows:
Python:
import numpy as np
import matplotlib
matplotlib.use("TkAgg")
import matplotlib.pyplot as plt
#################################################
# Parameter input
#################################################
hbar = 1.05e-34
h = 6.626e-34
m = 1
N = 400
a = 1
L = N * a
t = hbar**2 / ( 2 * m * a**2)
#################################################
# Parameter sanity check
#################################################
assert N%2 == 0, 'N must be an even number'
assert m > 0, 'Mass must be positive'
assert a > 0, 'Distance between points must be positive'
assert t >= 0, 'T must be non-negative. Make sure hbar is positive.'
#################################################
# Base code
#################################################
for i in range(0,100,10):
# Building the hamiltonian operator matrix and calculating its eigen
# values (eval) and eigen vectors (evec)
n = int(N/2)
a1 = np.full((N-1,), -t)
a2 = np.full((N,), 2*t)
Hamiltonian = np.diag(a1, -1) + np.diag(a2) + np.diag(a1, 1)
Hamiltonian[n,n] = Hamiltonian[n,n]- 1*10**i # Adds potential in middle.
eval, evec = np.linalg.eigh(Hamiltonian) # use .eig() if Hamiltonian is not symmetric
plt.plot(evec)
plt.show()For those amongst you who'd prefer a nicely formatted image of the assignment: https://puu.sh/yKp4D/b668471918.png
Attachments
Last edited: