Object Rotating on a Semicircle

[RoyalFlush100]

Homework Statement

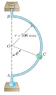
A small 700-g collar C can slide on a semicircular rod which is made to rotate about the vertical AB at a constant rate of 7.5 rad/s. The coefficients of friction are μs = 0.25 and μk = 0.20.
Determine the magnitude of the friction force exerted on the collar immediately after release in the position corresponding to θ = 75 degrees.

Pic attached below

Homework Equations

F = ma
an = d^2r/dt^2 - r(dθ/dt)^2

The Attempt at a Solution

I began by determining net acceleration.
a = (0.5 m)(7.5 rad/s)^2 = 28.125 m/s^2 pointed towards the center of the circle.
So the net force is going to equal (0.7 kg)(28.125 m/s^2) = 19.6875 N towards the center of the circle.

But I'm not sure what the FBD would look like in this case. I know that it'll have weight vertically down, but I am not sure how to set up the normal and frictional forces in this instance.

 

[kuruman]

But I'm not sure what the FBD would look like in this case. I know that it'll have weight vertically down, but I am not sure how to set up the normal and frictional forces in this instance.

The normal force is perpendicular to the surfaces being in contact. Its direction must be radial, either away or towards the center of the semicircle. The force of friction is tangent to the semicircle. It muSt be static friction because immediately after release, the collar has not started moving yet. However this force of static friction does not necessarily have its maximum value. Also, your number for the acceleration,

a = (0.5 m)(7.5 rad/s)^2 = 28.125 m/s^2

is incorrect. The circle that the collar describes is a horizontal circle, the radius of which is not the radius of the semicircle. Look at the drawing and imagine the collar spinning about the vertical axis. The normal force and the acceleration will be in the same direction only if θ = 90^o. Keep in mind that friction and the normal force are contact forces that adjust themselves to provide the observed acceleration, so start from figuring out what the correct acceleration is and then make sure that the sum of all the forces divided by the mass gives that acceleration.