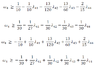Objective function of a linear program with multiple variables

[Yassineon]

Hello,
Please I need help to find the objective function of a linear program (attachement : example).
I tried to figure it out from the formula provided in (attachement : formula) but I couldn't understand it, it's written (MIN(lambda)wj) I think it's the key to my question ! ( Full file is attached too )
Any help as little as it could be, would be most welcomed!
Thanks in advance.

Moderator's note: Copyrighted article removed. Instead, here is the reference:
V. Vamitha et al., International Journal of Fuzzy Mathematics and Systems 2(3), 217-230 (2012)

 

[Timo]

I am not familiar with the notation around the min_lambda w_j ... . But given the statement starts with "for each j" and contains only one w_j the only sensible way to read this for me is "for each j, find a joint solution for w_j and the lambda_jk that minimizes w_j and obeys the additional constraints mentioned."

 

[Yassineon]

Thank you Very much Timo for your help, I appreciate it.
But I'm still confused about the objective function formula ...

 

[Ibix]

I'm also struggling with the notation, but it looks to me like you haven't shown us the objective function. They equations in the images all look like constraints to me - they're inequalities. The objective function looks to me to be $w_j$, which is presumably defined somewhere. Although defining constraints in terms of the objective function seems odd to me.

You don't have a link to the paper? A copy on arxiv.org, maybe?

 

[Yassineon]

Thank you very much Ibix for your time, actually this set of equations is from the multivariate markov's chain model, here is the link of the full text : https://www.ripublication.com/ijfms/ijfmsv2n3_02.pdf

 

[Timo]

If the objective is to minimize wj then suitable objective functions would be "f(wj) = wj", "f(wj) = 1.0 * wj" or "f(wj, {lambda_jk}) = 1.0 * wj + 0.0 * lambda_j1 + 0.0 * lambda_j2 + ...".

 

[Yassineon]

Thanks Timo for your response, well I already tried that objective function and tried also "0.0 * wj ..+ 1.0 * lambda_j1 + 1.0 * lambda_j2 + + 1.0 * lambda_j3 + 1.0 * lambda_j4 ". but couldn't get the same solution of the paper (((lambda's estimators for the inequalities that I posted are the 4th row of the solution attached)))
so it seems that it's another objective function.

 

[Timo]

Possibly. It could also be that there are multiple values for the lambda that lead to the same wj. Are your wj correct? Another option is that you made an error somewhere. I recommend to
1) Manually check that your solution satisfies the constraints. lambda>0 and sum(lambda)=1 can be seen directly from just looking at the numbers (-> the solution of the paper satisfies them); the other two relations are at least simple to verify.
2) Verify that you have the same Xj and B as the paper. On first glance, they are not explicitly given by the paper. So double-check your calculations.

And of course the paper could be wrong.

 

[Yassineon]

I really appreciate you help Timo, thanks a lot. for the points that you mentionned :

1) I didn't get lambda's that sum up to 1, I got some odd values, so I removed them all.
2) Yes that's the problem the paper tries to aggregate the results so they removed important steps for the solution, I was able to rewrite the other coefficients in the inequalities following the steps mentionned by the paper, but unfortunately I got different results.

As you said nothing proves that their results are right !