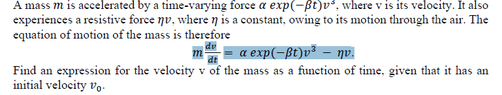SUMMARY
The discussion focuses on solving the ordinary differential equation (ODE) represented by the equation $$\frac{1}{v^3}\frac{dv}{dt}=-\frac{1}{2}\frac{dv^{-2}}{dt}$$. A working guide is requested for this equation, which can be approached using integrating factors. Additionally, it is clarified that aerodynamic force varies as the square of the velocity, not the cube, which is crucial for accurate modeling in physics.
PREREQUISITES
- Understanding of ordinary differential equations (ODEs)
- Familiarity with integrating factors in differential equations
- Knowledge of aerodynamic principles and their mathematical representations
- Basic calculus, specifically differentiation and integration
NEXT STEPS
- Study the method of integrating factors for solving ODEs
- Explore the relationship between velocity and aerodynamic force
- Review the tutorial on linear differential equations at tutorial.math.lamar.edu
- Investigate advanced ODE techniques, such as Laplace transforms
USEFUL FOR
Physicists, engineering students, and anyone involved in fluid dynamics or mathematical modeling of physical systems will benefit from this discussion.