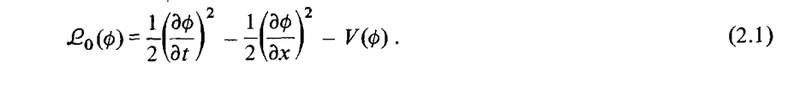One-dimensional field momentum

  • Thread starter Thread starter Independent
  • Start date Start date
  • Tags Tags
    Field Momentum
AI Thread Summary
The discussion centers on deriving the formula 4.8 from the Lagrangian in one spatial dimension, which relates to Noether's theorem and its implications for conserved quantities like energy and momentum. The canonical energy-momentum tensor is defined as Θ^{μν} and is derived from the Lagrangian density. The momentum density components are specified as Θ^{0j}, where j represents spatial dimensions. The conversation emphasizes the straightforward nature of demonstrating the formula based on these principles. Understanding these concepts is crucial for grasping the underlying physics of field momentum.
Independent
Messages
39
Reaction score
15
How does one arrive at the formula 4.8?
Screen Shot 2016-04-21 at 19.21.13.png


The Lagrangian (one spatial dimension) is:

Screen Shot 2016-04-21 at 19.22.24.png
 
Physics news on Phys.org
That's a special case of Noether's theorem for space-time translations, which is a symmetry of Minkowski space. The corresponding conserved quantities are energy and momentum. For fields it defines the canonical energy-momentum tensor
$$\Theta^{\mu \nu}=\frac{\partial \mathcal{L}}{\partial (\partial_{\nu} \phi)}\partial^{\mu} \phi-\mathcal{L} g^{\mu \nu}.$$
The momentum density components are given by ##\Theta^{0j}## (##j \in \{1,2,3 \}##). Now it should be easy to show the above formula.
 
  • Like
Likes Independent

Thread 'Is calling fictitious forces "not real" just about terminology?'

Hi there, im studying nanoscience at the university in Basel. Today I looked at the topic of intertial and non-inertial reference frames and the existence of fictitious forces. I understand that you call forces real in physics if they appear in interplay. Meaning that a force is real when there is the "actio" partner to the "reactio" partner. If this condition is not satisfied the force is not real. I also understand that if you specifically look at non-inertial reference frames you can...
View full post »

Thread 'Derivation of Hamilton's Principle: Questions'

I have recently been really interested in the derivation of Hamiltons Principle. On my research I found that with the term ##m \cdot \frac{d}{dt} (\frac{dr}{dt} \cdot \delta r) = 0## (1) one may derivate ##\delta \int (T - V) dt = 0## (2). The derivation itself I understood quiet good, but what I don't understand is where the equation (1) came from, because in my research it was just given and not derived from anywhere. Does anybody know where (1) comes from or why from it the...
View full post »

Similar threads

I Is there a way in Lagrangian mechanics to incorporate the inertial response from initial momentum when using initial conditions instead of BCs?
Replies
9
Views
988
I Lagrangian symmetry for the bullet and gun
Replies
7
Views
1K
I Lagrangian coordinate transformation (Noether)
Replies
11
Views
2K
I The effect of a field on a particle depends on the particle velocity?
Replies
5
Views
1K
Law of conservation of angular momentum
Replies
11
Views
12K
A Conflicting results about Stress tensor symmetry on EM field
Replies
18
Views
416
I Best book for Lagrangian of classical, scalar, relativistic field?
Replies
7
Views
2K
B The physics of flywheel launchers (like tennis ball shooters)
2
Replies
60
Views
4K
B Colliding balls: Conservation of momentum and changes in kinetic energy?
Replies
2
Views
2K
B Questions about momentum and force as well as normal force/friction
Replies
35
Views
4K

Hot Threads

Recent Insights

Back
Top