ichabodgrant
- 48
- 0
Member warned to use homework template
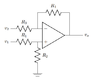
In the following circuit, compute the values of R1 and R3 in terms of R2 and R4, such that vo is always equal to v1 - 5v2.I have marked 3 nodes, A, B and C. v+ = v- as assumption for the op-amp.
Consider node A.
v- = v+ = v1 × (R2 / (R1+R2))
Consider node B and C.
(v- - v2) / R3 = (vo - v-) / R4
I now stick at here...
I can write R1 in terms of R2, but there exist v- and v1.
And for R3, the same problem exists.
First, is there anything wrong in my above computations?
Second, can I express R1 and R3 in terms of R2 and R4 without using other unknowns?
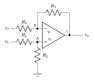
Consider node A.
v- = v+ = v1 × (R2 / (R1+R2))
Consider node B and C.
(v- - v2) / R3 = (vo - v-) / R4
I now stick at here...
I can write R1 in terms of R2, but there exist v- and v1.
And for R3, the same problem exists.
First, is there anything wrong in my above computations?
Second, can I express R1 and R3 in terms of R2 and R4 without using other unknowns?