jackscholar
- 73
- 0
θ
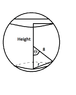
The attached diagram depicts a sphere with several variables: the height of the cylinder, the radius of the cylinder and an angle. All that has been given to me is the hypotenuse of a triangle used.
To my knowledge I was told to use 2sinθcosθ=sin2θ
Originally I attempted to get everything in terms of different variables and then substitute them into an equation to solve for one variable. Therefore, I used Pythagoras's Theorem and got:
8^2=y^2+r^2. I used y^2 to denote the unknown height within the triangle.
From here I used trigonometric functions and assumed the triangle was right angled. From here I got cosθ=y/8 and sinθ=r/8. And after this I tried substituting and it got very messy.
I tried substituting for one variable, then re-arranging both trig equations to get one variable and then I attempted to eliminate it to no avail.
Any help would be highly appreciate.
Homework Statement
The attached diagram depicts a sphere with several variables: the height of the cylinder, the radius of the cylinder and an angle. All that has been given to me is the hypotenuse of a triangle used.
Homework Equations
To my knowledge I was told to use 2sinθcosθ=sin2θ
The Attempt at a Solution
Originally I attempted to get everything in terms of different variables and then substitute them into an equation to solve for one variable. Therefore, I used Pythagoras's Theorem and got:
8^2=y^2+r^2. I used y^2 to denote the unknown height within the triangle.
From here I used trigonometric functions and assumed the triangle was right angled. From here I got cosθ=y/8 and sinθ=r/8. And after this I tried substituting and it got very messy.
I tried substituting for one variable, then re-arranging both trig equations to get one variable and then I attempted to eliminate it to no avail.
Any help would be highly appreciate.