Optimizing Range in Projectile Motions: Analyzing Launch Angle Graphs

[Temper888]

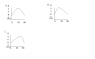
1. Which of the following graphs BEST depicts the relationship between launch angle and range in the experiment?Please explain how you arrived to the answer.

Attached is the graphs and the Experiment model.3.I guessed it to be either Graph B or Graph C, but I am not sure.

 

[mtayab1994]

What is the angle that you shot the slingshot at?

 

[technician]

Do you know what angle to fire a projectile to get maximum range (simplest case!)

 

[Temper888]

I know the maximum range angle would be 45 because of the equation: R=v^2sin2θ/g.

 

[Temper888]

Tayab,

There is no specific angle.The question is asking what happens to the range if the launch is increased? From equation R=v^2sin2θ/g, it can be said that range increases until the angle increases to 45 and then decreases from 45 and above because of sin2θ. The graph for range vs. launch angle should be a symmetrical upside-down parabola for same initial and final heights. However, I cannot figure out how does different initial and final heights as in this experiment affect the symmetry of that parabola?