woodywheel
- 15
- 0
Homework Statement
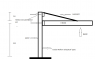
I am trying to design a workshop crane and have found a considerable success so far. It is a maximum 2 ton crane and i have found which I beam to use by the method mentioned below.
Some of the specifications are
boom length(span) = 3 m
mast length(vertical portion) = 4 m
the boom is connected at 3m height remaining 1m to fix a support
I beam of 250x125x6/9 used has a yield point of 350 N/mm2, where 6mm is web thickness and 9 is flange thickness.
the beam will be welded to a round bar(with a pin inside) which in turn will be connected to a flange that again be welded to the mast. the calculation done is by taking into consideration if I beam is fixed at one end. My doubts are below
1.how can I find factor of safety here(dividing experimental by theoretical yield stress?? )
2. i want to fix a support on the boom of the crane which will be connected to vertical portion or mast of the crane which will be joined above the connecting point of boom, but i am not able to decide the exact location to connect the support on the boom. I am resolving forces here and there but i want the optimum position and angle of the support.
3.any good literature on the internet i can find
Homework Equations
Bending Moment= FxL
Second moment of inertia for I beam= (bh^3-(b-tw)xh1^3)/12
and bending Force is F/y=M/I
The Attempt at a Solution
Bending Moment= 5880 Nm
I= 333783168 mm^4
Bending stress= 21.7 N/mm^2
even my bending stress is 21.7 and selected I beam has a yield point of 350 N/mm^2
Attachments
Last edited: