dlp248
- 8
- 0
Homework Statement
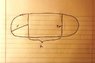
Maximize the area (in feet) of the rectangular field inside of a mile long racetrack.
Homework Equations
Circumference of a circle = 2πr
P= 2x + 2y
The Attempt at a Solution
Area of the semicircles = πr^2
Area of the rectangle = 2rh
A(r) = πr^2 +2rh
P= 2πr + 2h + 4r
5280ft = 2πr + 2h + 4r
h= 2640 - πr - 2r
A(r) = πr^2 + 2r(2640 - πr - 2r)
A(r) = πr^2 + 5280r - 2πr^2 - 4r^2
A(r) = 5280r - πr^2 - 4r^2
A'(r) = 5280 - 2πr -8r
0 = 5280 - 2πr -8r
2πr + 8r = 5280
r(2π + 8) = 5280
r = 5280/(2π + 8) ft
r ≈ 369.67 ft
A"(r) = -2π - 8
A"(r) < 0
r is a maximum
h = 2640 - (5280/(2π + 8))π - 2(5280/(2π + 8))
h = 10560/(2π + 8) ft
h ≈ 739.33 ft
A(r) = πr^2 +2rh
A(r) = π(5280/(2π + 8) ft)^2 + 2((5280/(2π + 8) ft)(10560/(2π + 8) ft))
A(r) ≈ 975,917 ft^2
I believe this answer is incorrect because for the perimeter, I included the two diameters of the semicircles (the width of the imaginary rectangle). So I ended up using part of the given distance to make these sides and my perimeter formula does not represent the actual perimeter of the track. I tried to redo this problem just using:
P= 2πr + 2h
however this formula produces an r value that makes the h value equal zero. Obviously I am missing a small detail and I have no idea what it is!
Last edited: