Ordinals .... Searcoid, Corollary 1.4.5 .... ....

[Math Amateur]

I am reading Micheal Searcoid's book: "Elements of Abstract Analysis" ... ...

I am currently focused on understanding Chapter 1: Sets ... and in particular Section 1.4 Ordinals ...

I need some help in fully understanding the Corollary to Theorem 1.4.4 ...

Theorem 1.4.4 and its corollary read as follows:

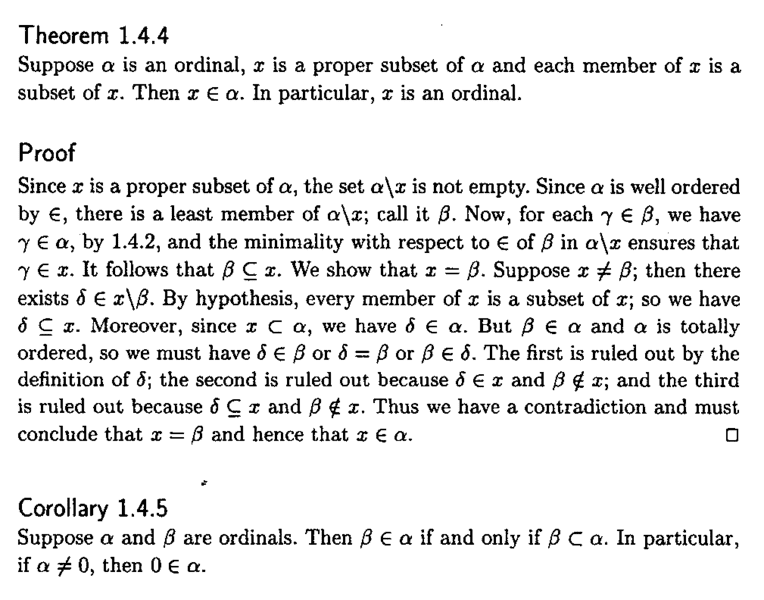
Searcoid gives no proof of Corollary 1.4.5 ...

To prove Corollary 1.4.5 we need to show $\beta \in \alpha \Longleftrightarrow \beta \subset \alpha$ ... ...
Assume that $\beta \in \alpha$ ...

Then by Searcoid's definition of an ordinal (Definition 1.4.1 ... see scanned text below) we have $\beta \subseteq \alpha$ ...

But it is supposed to follow that $\beta$ is a proper subset of $\alpha$ ... !

Is Searcoid assuming that $\beta \neq \alpha$? ... ... if not how would it follow that \beta \subset \alpha ... ?
Hope someone can help ...

Peter

============================================================================It may help readers of the above post if the start of the section on ordinals was accessible ... so I am providing that text as follows:

Hope that helps ...

Peter

 

[andrewkirk]

For the forward direction $\Rightarrow$ of the equivalence $\Leftrightarrow$, having $\beta=\alpha$ together with $\beta\in\alpha$ would give us $\alpha\in\alpha$, which would contradict Theorem 1.4.3.

For the reverse direction we just use $\beta\subset\alpha\to \beta\subseteq\alpha$ and proceed from there.

 

[Math Amateur]

Thanks Andrew ...

Just another question ... the Corollary goes on to state that, in particular, if $\alpha \neq 0$ then $0 \in \alpha$ ... can you help with the proof of this ... ?Thanks again,

Peter

 

[andrewkirk]

0 is the empty set, which is a subset of every set, so in particular $0\subseteq\alpha$. Putting this together with $\alpha\neq 0$ gives $0\subset\alpha$. Applying the corollary to that with the arrow pointing left gives us $0\in\alpha$.

 

[Math Amateur]

Thanks Andrew,

Peter