coltson
- 9
- 0
Homework Statement
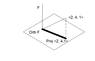
Being F = (1,1,-1), the orthogonal projection of (2,4,1) over the orthogonal subspace of F is:
a) (1,2,3)
b) (1/3, 7/3, 8/3)
c) (1/3, 2/3, 8/3)
d) (0,0,0)
e) (1,1,1)
The correct answer is B
Homework Equations
The Attempt at a Solution
Using the orthogonal projection formula:
(1,1,-1).(2,4,-1) * (1,1,-1) = 7/3 * (1,1,-1) = (7/3,7/3,-7/3)
(1,1,-1).(1,1-1)
I am obviously misunderstanding something, I thought that maybe orthogonal subspace ain't (1,1-1), but the answer makes me believe that I should have (1,1-1) in the formula.
Last edited by a moderator: