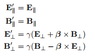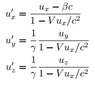Paradox - different results for different viewers

[kajagoooooooo]

Homework Statement

One person that we will call him - A is standing on an infinite charged non conductive panel with velocity V=(-Vx0,0).
A is throwing a particle q with V=(Vx0,Vy0).
The other person - B, is start running below the particle at t=t0.
A thinks that B will see the particle above him all the time because their both x velocity`s is not changing the whole time.
But if B calculate the route of the particle, while he is taking into account the magnetic field because of the moving charged panel he gets a magnetic force: Fb=(-F,0), so the particle accelerate to y and to -x.
Why they don`t calculate the same route? both inertial systems.

Homework Equations

Coulomb law.

3. The Attempt at a Solution
I don`t have an idea what the solution might be.

 

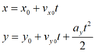
[TSny]

Stick with A's frame for the moment. Which of the following is true?

(a) the x-component of the momentum of the particle is constant in A's frame
(b) the x-component of the velocity of the particle is constant in A's frame
(c) both are constant
(d) neither is constant

Also, it would help to clarify the orientation of the panel. Is the y-axis perpendicular to the panel so that the E field is in the y direction?

 

[kajagoooooooo]

Stick with A's frame for the moment. Which of the following is true?

(a) the x-component of the momentum of the particle is constant in A's frame
(b) the x-component of the velocity of the particle is constant in A's frame
(c) both are constant
(d) neither is constant

both are constant.
But A thinks that for B`s point of view the x-component of the velocity is zero.
But when you go inside B`s inertial system, he thinks that the particle has V=(-Vx,0) because of the magnetic force.

 

[TSny]

both are constant.

No.

Can you state the relativistic formula for the x-component of momentum of the particle in terms of mass and velocity?

 

[kajagoooooooo]

In A system:

In B system:

 

[TSny]

The resolution of the paradox involves relativity.

Is this the correct setup of the problem at the moment the particle is launched?

A's frame is the unprimed frame and B's frame is the primed frame.

 

[kajagoooooooo]

The resolution of the paradox involves relativity.

Is this the correct setup of the problem at the moment the particle is launched?
View attachment 214118

A's frame is the unprimed frame and B's frame is the primed frame.

Yes it is the setup.
If you can solve it using relativity it would be great!

 

[TSny]

Yes it is the setup.
If you can solve it using relativity it would be great!

It's your problem .

The magnetic force in B's frame will give the particle a nonzero x-component of acceleration. Does the particle also have a nonzero x-component of acceleration in A's frame where there is no x-component of force? You can answer that by considering the relativistic formula for the x-component of momentum.

 

[kajagoooooooo]

It's your problem .

The magnetic force in B's frame will give the particle a nonzero x-component of acceleration. Does the particle also have a nonzero x-component of acceleration in A's frame where there is no x-component of force? You can answer that by considering the relativistic formula for the x-component of momentum.

I think I got it.
If I look at the system from the point of view of A itself, and then use this formulas:

I get a force on the x-component too!

 

[TSny]

In A's frame, the only force is the electric force, qE, in the y direction. There is no magnetic field in A's frame.

So, the x-component of force is zero in frame A.

The key is to recall whether force in relativity is equal to rate of change of momentum or equal to mass times acceleration.

 

[kajagoooooooo]

In A's frame, the only force is the electric force, qE, in the y direction. There is no magnetic field in A's frame.

So, the x-component of force is zero in frame A.

The key is to recall whether force in relativity is equal to rate of change of momentum or equal to mass times acceleration.

I don`t get it,
Why there will be any change of momentum in frame A?

 

[TSny]

In frame A the x-component of the force is zero. This means that the x-component of momentum is constant. But that implies that the x-component of velocity decreases in this situation where the particle’s y- component of velocity increases. To see why, look at the formula for the x-component of momentum. It involves both the x- and y- components of velocity.

 

[kajagoooooooo]

In frame A the x-component of the force is zero. This means that the x-component of momentum is constant. But that implies that the x-component of velocity decreases in this situation where the particle’s y- component of velocity increases. To see why, look at the formula for the x-component of momentum. It involves both the x- and y- components of velocity.

Thanks!
For those who are searching for the formula:

 

[TSny]

Thanks!
For those who are searching for the formula:
View attachment 214186

These are the formulas for transforming velocity from the unprimed frame to the primed frame.

The relativistic formula for momentum is given by the last equation here http://www.saburchill.com/physics/chapters/0093.html

 

[kajagoooooooo]

These are the formulas for transforming velocity from the unprimed frame to the primed frame.

The relativistic formula for momentum is given by the last equation here http://www.saburchill.com/physics/chapters/0093.html

Sorry for the misunderstanding,
But if Vx0=0 at the beginning of the question, isn`t Px will stay 0 the entire time?
Maybe we multiply bigger number, but we multiply it by zero (Vx0).

 

[TSny]

Sorry for the misunderstanding,
But if Vx0=0 at the beginning of the question, isn`t Px will stay 0 the entire time?

Yes, that's right. If V_x0 = 0 and if there is no x-component of force, then V_x and P_x will remain zero. But in A's frame, V_x0 is not zero.

According to A, V_x must decrease in order to maintain a constant x-component of momentum. This sounds paradoxical at first, until you examine carefully the formula for the x-component of relativistic momentum. Note, that if you use the concept of relativistic mass: m_r = m/(1-V²/c²)^1/2, then you can write the x-component of momentum as

P_x = m_rV_x.

As the particle pick up speed in the y-direction due to the electric force, what happens to the relativistic mass? So, what must happen to V_x in order for P_x to remain constant? (Remember, in A's frame there is no force acting on the particle in the x direction. So, in A's frame P_x is constant.)

In B's frame, V'_x0 = 0. As time passes according to B, V'_x will decrease (become more and more negative) due to the magnetic force acting in the negative x direction.

Both frames agree that the particle has nonzero x-component of acceleration. (But, they will disagree on the numerical value of the acceleration.)

 

[kajagoooooooo]

Yes, that's right. If V_x0 = 0 and if there is no x-component of force, then V_x and P_x will remain zero. But in A's frame, V_x0 is not zero.

According to A, V_x must decrease in order to maintain a constant x-component of momentum. This sounds paradoxical at first, until you examine carefully the formula for the x-component of relativistic momentum. Note, that if you use the concept of relativistic mass: m_r = m/(1-V²/c²)^1/2, then you can write the x-component of momentum as

P_x = m_rV_x.

As the particle pick up speed in the y-direction due to the electric force, what happens to the relativistic mass? So, what must happen to V_x in order for P_x to remain constant? (Remember, in A's frame there is no force acting on the particle in the x direction. So, in A's frame P_x is constant.)

In B's frame, V'_x0 = 0. As time passes according to B, V'_x will decrease (become more and more negative) due to the magnetic force acting in the negative x direction.

Both frames agree that the particle has nonzero x-component of acceleration. (But, they will disagree on the numerical value of the acceleration.)

Thanks!
You're the best!

 

[Kajagoogooooooo]

Yes, that's right. If V_x0 = 0 and if there is no x-component of force, then V_x and P_x will remain zero. But in A's frame, V_x0 is not zero.

According to A, V_x must decrease in order to maintain a constant x-component of momentum. This sounds paradoxical at first, until you examine carefully the formula for the x-component of relativistic momentum. Note, that if you use the concept of relativistic mass: m_r = m/(1-V²/c²)^1/2, then you can write the x-component of momentum as

P_x = m_rV_x.

As the particle pick up speed in the y-direction due to the electric force, what happens to the relativistic mass? So, what must happen to V_x in order for P_x to remain constant? (Remember, in A's frame there is no force acting on the particle in the x direction. So, in A's frame P_x is constant.)

In B's frame, V'_x0 = 0. As time passes according to B, V'_x will decrease (become more and more negative) due to the magnetic force acting in the negative x direction.

Both frames agree that the particle has nonzero x-component of acceleration. (But, they will disagree on the numerical value of the acceleration.)

My teacher solved this question today at class using the "hidden momentum",
Can you put a little bit of light between 400nm to 700nm wavelength on this solution so that I will be able to realize this too?

Thanks,
Kaja

 

[TSny]

My teacher solved this question today at class using the "hidden momentum",
Can you put a little bit of light between 400nm to 700nm wavelength on this solution so that I will be able to realize this too?

I think this request is too vague. Can you show the solution given by your teacher and indicate specifically where you are having difficulties?