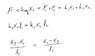Parallel Springs subject to load

[pige]

Homework Statement

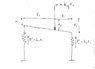
A system of two springs is considered, with spring constants k1 and k2, arranged in parallel and attached to a massless rigid bar. The bar remains horizontal when no force on it is zero. Determine the equivalent spring constant (ke) that relates the force applied a distance l1 from one spring and l2 from the other (F is between the springs) to the resulting displacement for small oscillations

Homework Equations

F1=k1*x1
F2=k2*x2

F=ke*x
sin(theta)=theta
U=1/2*k*x^2

T=F*R

The Attempt at a Solution

It was decided after much group work to try and use energy. We ended up setting the potential energy of the two springs to the potential energy of the equivalent spring. Using the small angle approximation we could write the angular displacements as the displacement of the springs due to the rotation, but weren't able to derive an expression for the translational displacement of the bar, and thus not able to get an expression for the total spring compression.

 

[Spinnor]

A picture would help.

 

[Died37]

A picture would help.

 

[Spinnor]

The force F causes the two springs to compress until equilibrium is reached. At that point the sum of the forces in the vertical direction sum to zero. Also the sum of the torques about the point the force F is applied is zero.

 

[Spinnor]

The force F causes the two springs to compress until equilibrium is reached. At that point the sum of the forces in the vertical direction sum to zero. Also the sum of the torques about the point the force F is applied is zero.

That may be true but it is not enough.

You get three relationships, sum forces in vertical = 0, sum of torques about the point of applied force F = 0, and a geometrical relationship between x1, x2, and x,3. See below. Solve for ke.