zicron
- 6
- 0
1. Find the length of the curvature of a concave mirror of 20cm that comply with paraxial approximation for all incident rays
2.conventional geometry formula , sinθ≈θ or tanθ≈θ for paraxial rays
3. I had try drafting out the diagram , labeling all the unknown angle with symbol and trying to work out on them but I just can't find the angle CAB of the triangle because I don't know height of the triangle.
This is a sketch:
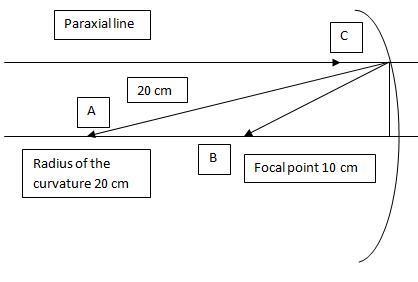
Did I miss anything?
Any suggestion on how to solve this problem?
2.conventional geometry formula , sinθ≈θ or tanθ≈θ for paraxial rays
3. I had try drafting out the diagram , labeling all the unknown angle with symbol and trying to work out on them but I just can't find the angle CAB of the triangle because I don't know height of the triangle.
This is a sketch:
Did I miss anything?
Any suggestion on how to solve this problem?