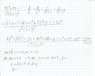jegues
- 1,085
- 3
Homework Statement
I'm just curious if there is any useful shortcuts when applying partial fractions decomposition. These are only a portion of the problem given for us, so it's important that I can do them quickly and efficiently.
Does anyone know of any useful shortcuts that would speed up the process?
I posted and example of one of the decompositions we are expected to face in typical problem.
Homework Equations
N/A.
The Attempt at a Solution
See figure for example.