Justin_Lahey
- 1
- 0
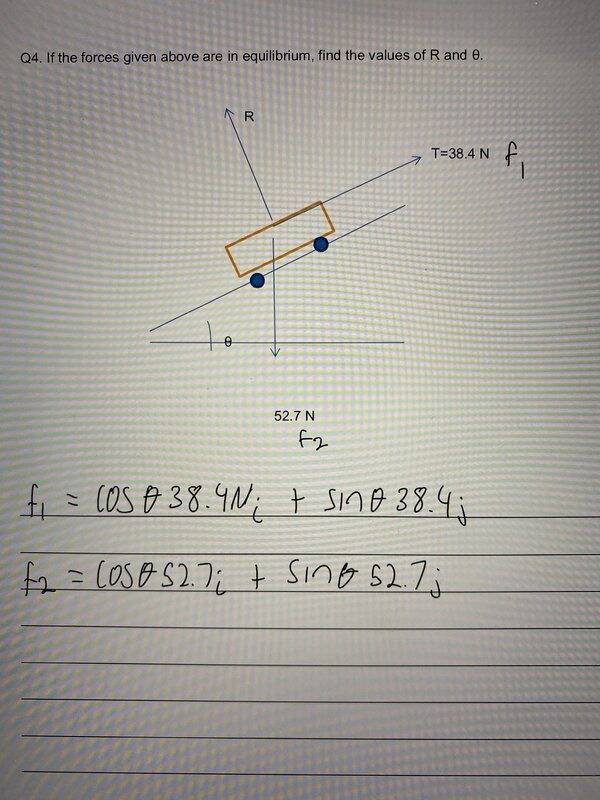
- Homework Statement
- Find the magnitude and angle
- Relevant Equations
- F1= cos(theta)38.4i+ sin(theta)38.4j
F2= cos(theta)52.7i + sin(theta)52.7j
Hi, I’m wondering if someone can help me understand this question. I can find a resultant force/vector when given an initial angle but I’m stuck here when the only information is the two magnitudes. I think I’m solving for the unknowns but a little lost on how or what equation I should be using. In the pic this is how I normally start by finding the x and y components but without theta I’m a bit lost. Thanks for any help.
Last edited by a moderator: