Particle sliding down a hemispherical bowl

[Tanya Sharma]

Homework Statement

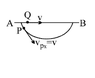
A particle P is sliding down a frictionless hemispherical bowl. It passes the point A at t = 0. At this instant of time, the horizontal component of its velocity is v. A bead Q of the same mass as P is ejected from A at t=0 along the horizontal string AB, with the speed v. Friction between the bead and the string may be neglected.Which bead reaches point B earlier?

Homework Equations

The Attempt at a Solution

Let θ be the angle which the particle P makes with the vertical .

N-Mgcosθ = Mv²/R

Mgsinθ = -Mvdv/dx

or,Mgsinθ = -Mvdv/Rdθ

RMgsinθdθ = -Mvdv

∫_β⁰RMgsinθdθ = -∫_u^wMvdv , where β is the initial angle ; u is the initial velocity and w is the velocity at the bottommost point .

But how to relate initial velocity 'u' with the initial horizontal component of velocity 'v' .

I am not sure if this is the correct approach.

I would be grateful if someone could help me with the problem.

 

[Chestermiller]

Hi Tanya,

N is not constant. You need to do the force balance in the tangential direction, not the radial
direction.

Chet

 

[dauto]

Use energy conservation

 

[TSny]

Does either particle have a horizontal component of acceleration?

 

[Tanya Sharma]

Hi Tanya,

N is not constant. You need to do the force balance in the tangential direction, not the radial
direction.

Chet

Hi Chet...

I might have made some mistake , but I think I have written force equation in tangential direction in post#1.Are you trying to convey something else ?

 

[Tanya Sharma]

Does either particle have a horizontal component of acceleration?

Hello TSny

here is my reasoning...

There is a component of normal Nsinθ in horizontal direction .Even though the magnitude of this force decreases as the particle slides down ,still it accelerates the particle in horizontal direction till it reaches the bottom .The horizontal component of velocity at any instant during the downward journey ,say v_P,x will be greater than 'v' .

During the upward journey,it is the same component of normal force Nsinθ which decelerates the particle , till it reaches the opposite point to the initial point.Here either by conservation of energy or by symmetry we can say that the velocity of the particle will be same as that of the initial point .

So we can infer that the horizontal component of velocity will always be greater than 'v' during the entire journey. v_P,x >v . The average horizontal speed of the particle is greater than 'v' .

OTOH in case of Q there is no horizontal acceleration,hence velocity of v_Q = v .

The horizontal distances are same in both the cases ,hence t_P < t_Q

Does this make sense ?

 

[TSny]

here is my reasoning...

There is a component of normal Nsinθ in horizontal direction .Even though the magnitude of this force decreases as the particle slides down ,still it accelerates the particle in horizontal direction till it reaches the bottom .The horizontal component of velocity at any instant during the downward journey ,say v_P,x will be greater than 'v' .

During the upward journey,it is the same component of normal force Nsinθ which decelerates the particle , till it reaches the opposite point to the initial point.Here either by conservation of energy or by symmetry we can say that the velocity of the particle will be same as that of the initial point .

So we can infer that the horizontal component of velocity will always be greater than 'v' during the entire journey. v_P,x >v . The average horizontal speed of the particle is greater than 'v' .

OTOH in case of Q there is no horizontal acceleration,hence velocity of v_Q = v .

The horizontal distances are same in both the cases ,hence t_P < t_Q

Does this make sense ?

Excellent!