Pendulum/Circular Motion Problem

[Jay0078]

Homework Statement

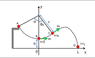
A small ball of mass m is attached to a very light string of length L that is tied to a peg at
point P. What is the magnitude of the horizontal velocity that must be applied to the ball
so that it swings up and lands on the peg? Your answer can only contain the given
information and any appropriate physical constants (such as g).
If you have the acceleration of gravity g in your answer do not
substitute numbers for it. You may introduce other variables to
help you reach a solution but your final solution can only
contain the given variables and g.
(SEE ATTACHED)

Homework Equations

Conversation of Mechanical Energy?

The Attempt at a Solution

My initial thought was to set ΔK=ΔP since gravity is a conservative force and the only displacement is vertically, the length of the string. That gave me an initial velocity of √2gL

 

[paisiello2]

Your solution only gets the ball horizontal with the peg. You need to give it more speed to cause it to land on top of the peg.

 

[Jay0078]

Exactly. Thanks for the reply. I found an initial velocity to make a complete revolution also, which is not what I'm looking for. Any ideas anyone?

 

[paisiello2]

And what velocity is that?

 

[haruspex]

Exactly. Thanks for the reply. I found an initial velocity to make a complete revolution also, which is not what I'm looking for. Any ideas anyone?

Clearly the answer lies between those two extremes.
You need the string to go slack at some point above the horizontal, but before the vertical.
Suppose it goes slack at angle θ above the horizontal. What initial velocity would lead to that (as a function of θ)? What will the subsequent trajectory be?

 

[Jay0078]

And what velocity is that?

√(2gL) ≤v_0≤ 2√(gL)

 

[Jay0078]

Clearly the answer lies between those two extremes.
You need the string to go slack at some point above the horizontal, but before the vertical.
Suppose it goes slack at angle θ above the horizontal. What initial velocity would lead to that (as a function of θ)? What will the subsequent trajectory be?

Could I relate that to the tension in the string? Or centripetal acceleration?

 

[paisiello2]

√(2gL) ≤v_0≤ 2√(gL)

How did you come up with that?

 

[dauto]

Could I relate that to the tension in the string? Or centripetal acceleration?

Yes, when the string goes slack the tension becomes________.

 

[Jay0078]

Yes, when the string goes slack the tension becomes________.

Right, I'm just trying to find a way to relate them mathematically without introducing unnecessary variables because the solution can only contain the given variables.

 

[haruspex]

Right, I'm just trying to find a way to relate them mathematically without introducing unnecessary variables because the solution can only contain the given variables.

It is often appropriate to introduce extra variables, then find enough equations to eliminate them. I would certainly recommend introducing one for the angle at which the string goes slack.

 

[Jay0078]

I'm needing some direction. I realize that at some point after the horizontal the string must go slack; at this point it seems to be a projectile motion problem with a displacement in the x direction (L). Any thoughts?

 

[Jay0078]

It is often appropriate to introduce extra variables, then find enough equations to eliminate them. I would certainly recommend introducing one for the angle at which the string goes slack.

How would I do that?

 

[Jay0078]

It is often appropriate to introduce extra variables, then find enough equations to eliminate them. I would certainly recommend introducing one for the angle at which the string goes slack.

Vo=√(2gL(1-cosΘ))

How am I coming along? I'm working on finding a way to relate Θ back to the velocity needed to get the ball back to the peg.

 

[haruspex]

Vo=√(2gL(1-cosΘ))

No, that's the speed needed to reach that height. But if the string is to stay taut it must be supplying (some nonzero portion of) the centripetal force. Consider the forces when in this position. What speed is it moving at if it's still moving in a circle but the string tension is just reaching zero.

 

[mpresic]

I got a ratio of L to r, but I would not swear it is correct. Is the answer given in the back of the book or something, to work towards? (actually looking at your thumbnail, I find I did a related (equivalent) problem, not this one)

 

[haruspex]

I got a ratio of L to r, but I would not swear it is correct. Is the answer given in the back of the book or something, to work towards? (actually looking at your thumbnail, I find I did a related (equivalent) problem, not this one)

r? What distance is that?

 

[mpresic]

I did the problem where it is released horizontally from height L, and hits a peg at L - r, so that r is the radius of the path. The mass does not make the orbit with radius r but the tension goes to zero at some angle. After the tension hits zero, the mass goes on a parabolic path to the peg. This may make the problem even harder.

 

[Jay0078]

No, that's the speed needed to reach that height. But if the string is to stay taut it must be supplying (some nonzero portion of) the centripetal force. Consider the forces when in this position. What speed is it moving at if it's still moving in a circle but the string tension is just reaching zero.

I got v=√(gL) for the tension just going to zero at the top.

 

[Jay0078]

I got a ratio of L to r, but I would not swear it is correct. Is the answer given in the back of the book or something, to work towards? (actually looking at your thumbnail, I find I did a related (equivalent) problem, not this one)

No, I have searched and searched. However, I did find a tarzan-physics problem that had to do with rotation and projectile motion. It seemed fairly complex though it may be helpful.

http://arxiv.org/pdf/1208.4355.pdf

 

[haruspex]

I got v=√(gL) for the tension just going to zero at the top.

Sure, but we don't need it taut at the top.
In your post #14, you seem to have taken theta as the angle traversed from starting position, so I'll stick with that.
Draw a free body diagram for the mass when the string tension just reaches zero, so it's still moving in a circle (just). What forces act on the mass? Suppose it is moving at speed v_θ. What is the component of its acceleration towards the anchor point? What equation does that give you?