Understanding Periodic Motion: Proving and Explaining its Repeating Nature

[ChiralSuperfields]

Homework Statement

A ball dropped from a height of 4.00 m makes an elastic collision with the ground. Assuming no mechanical energy is lost due to air resistance, show that
the ensuing motion is periodic.

Relevant Equations

1-D Kinematic equation

For part (a) of this problem,

The solution is,

However why did say show the motion is periodic, but then the solutions don't show it, instead explain how it is periodic?

Is there a way to prove that the motion is periodic other than the solution to part (b)?

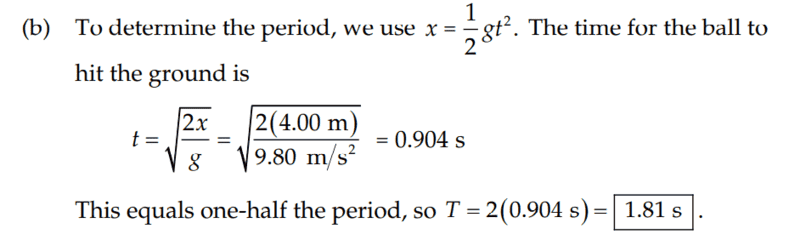
Many thanks!

 

[haruspex]

What do you think periodic means?

 

[ChiralSuperfields]

What do you think periodic means?

Time taken for 1 cycle of a motion.

 

[haruspex]

Time taken for 1 cycle of a motion.

No, that's the period if it is periodic. How do you decide whether a motion is periodic?

 

[malawi_glenn]

Time taken for 1 cycle of a motion.

No, that is called "the period".
What does periodic (motion) mean? And why do you think the motion of the ball in this problem is a periodic motion.

 

[ChiralSuperfields]

Thank you @haruspex and @malawi_glenn for your replies! A motion is periodic when the period of each cycle is the same. I think the motion is periodic in this case because mechanical energy is conserved as there are no non-conservative forces acting so the max height will be the same each cycle.

Kind regards,
Callum

 

[malawi_glenn]

instead explain how it is periodic?

the motion is periodic in this case because mechanical energy is conserved as there are no non-conservative forces acting so the max height will be the same each cycle.

spot on bro!

 

[ChiralSuperfields]

spot on bro!

Thank you @malawi_glenn!

 

[malawi_glenn]

Thank you @malawi_glenn!

Now to be more precise regarding the periodic motion of this ball. What can you say about the time for one cycle? The ball will reach same max height each bounce. How does that affect the time of each cycle?

 

[jbriggs444]

A motion is periodic when the period of each cycle is the same.

It is important that the motion actually have a cycle. The definition of "periodic" should include that. When in doubt, Google "periodic definition" or "periodic definition mathematics". You can get hits such as this one.

 

[kuruman]

A motion is periodic when the period of each cycle is the same.

I concur with @jbriggs444. Can you come up with a sharper definition? How do you define "the same"? What if the motion is complicated? For example, the picture shows the readings of an electrocardiogram (EKG). Is the heartbeat as evidenced by the EKG periodic? What makes, or doesn't make, it so?

 

[ChiralSuperfields]

A motion is periodic when the period of each cycle is the equal. A cycle of the motion starts and ends at the same point which can be arbitrarily chosen.

I think the EKG is periodic because it starts and ends at the same point and the period is the same for each cycle.

Is that better?

Many thanks!

 

[kuruman]

I agree that the EKG is periodic, but you're not there yet.

What starts and ends? What same point? Time increases to the right on the horizontal axis and no point on it is the "same" as some other point on it. The vertical axis is voltage.

 

[ChiralSuperfields]

I agree that the EKG is periodic, but you're not there yet.

What starts and ends? What same point? Time increases to the right on the horizontal axis and no point on it is the "same" as some other point on it. The vertical axis is voltage.

Thank you @kuruman for your reply!

I tried to draw what I think is the period of the EKG,

The period will be the same as long as you find the same points each cycle, for example,

.

So when I mean by the 'same' points (coordinates on the EKG graph) in that they have the same voltage values, but different time values. The difference between the finial and initial time values for the same voltage is the definition of the period, correct?

Many thanks,
Callum

 

[berkeman]

So when I mean by the 'same' points (coordinates on the EKG graph) in that they have the same voltage values, but different time values. The difference between the finial and initial time values for the same voltage is the definition of the period, correct?

You are definitely on the right track, but there is one final step that we all want you to take to use the standard test for a periodic waveform, as hinted about by this reply:

It is important that the motion actually have a cycle. The definition of "periodic" should include that. When in doubt, Google "periodic definition" or "periodic definition mathematics". You can get hits such as this one.

Can you write the fundamental equation that defines periodic behavior based on that article?

 

[ChiralSuperfields]

You are definitely on the right track, but there is one final step that we all want you to take to use the standard test for a periodic waveform, as hinted about by this reply:Can you write the fundamental equation that defines periodic behavior based on that article?

Thanks for your reply @berkeman! I found after some research, that a period function must have the following property:

Where P = the period of the function and n = non-zero integers.

To me all that equation is really saying at that for a function to be periodic, there must be at least two x-values that have the same y-value. But then that would include parabolas?

I don't think parabolas are considered periodic functions, so I think the correct interpretation is that there must be a domain of x-values which have the same y-value.

Many thanks!

 

[berkeman]

I don't think parabolas are considered periodic functions, so I think the correct interpretation is that there must be a domain of x-values which have the same y-value.

The parabolic y value versus time of a bouncing ball with no energy loss in the bounces (coefficient of restitution = 1.00) is definitely periodic, which you can show with that equation.

 

[kuruman]

Good work! Now what would an appropriate $f(x)$ look like for the bouncing ball that got this thread rolling? What would $x$ and $P$ be? Be as specific as you can, and you may define extra variables if you feel you need them.

 

[berkeman]

for the bouncing ball that got this thread rolling?

Uh-oh, vertigo, I'm getting dizzy...

 

[ChiralSuperfields]

Thank you @berkeman and @kuruman !

How cool!

Many thanks!

 

[berkeman]

Good work. Note also that the plus sign in your equation can be replaced by $\pm$ in this case, since the parabola is symmetric forward and backward in time. That won't always be the case for periodic functions.

 

[jbriggs444]

To me all that equation is really saying at that for a function to be periodic, there must be at least two x-values that have the same y-value. But then that would include parabolas?

That equation says that for every x, there are infinitely many other x-values that have the same y-value. Those x values are x+p, x+2p, x+3p, ... along with x-p, x-2p, x-3p, ...

So you can take a snapshot of one period of the graph, slide it over by one period and have something identical to the snapshot of the next period.

Now then, you quote an equation which says that the period is:$$P=\sqrt{\frac{2h}g}$$But that period is the time to fall from rest to ground. If you take a snapshot of that much of the graph and slide it over by one period, does it match the next piece of the graph?

 

[kuruman]

I believe the period should be $P=2\sqrt{\frac{2h}{g}}$, i.e. twice the time it takes to reach the ground from height $h$. To complete the cycle, it has to go back to the release height.

 

[ChiralSuperfields]

Ok thank you @berkeman, @jbriggs444, @kuruman for your replies! Sorry, yes, the period should be

.

 

[malawi_glenn]

I would just say that if t=0 is the time the ball was dropped at rest from the height h, the ball will get back at the height h and have speed 0 at t = P.
Periodic motion is same position and same velocity when the time P has elapsed.

 

[ChiralSuperfields]

I would just say that if t=0 is the time the ball was dropped at rest from the height h, the ball will get back at the height h and have speed 0 at t = P.
Periodic motion is same position and same velocity when the time P has elapsed.

Ok thank you @malawi_glenn !