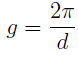You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
I Periodic potential V(x) -- how can I show that the period is d?
Mathematics news on Phys.org
- 32,814
- 4,725
GAB1 said:
for cos (2πx/d), change the values of x in terms of d, i.e. 0.1d, 0.2d ... etc... When do you get the full cycle?
BTW, this is math, not physics.
Zz.
RPinPA
Science Advisor
Homework Helper
- 587
- 329
If ##f(x)## has a period of ##d## then ##f(x) = f(x + d)## for all ##x##.
Change ##x## to ##x + d##. See what happens.
I should note that this only establishes the ##d## is a period. If you shift a sine wave of period ##T## by 10 periods, you get the same sine wave, so ##10T## is a period but not the smallest period. You have to do a little more reasoning to establish that ##d## is the smallest period.
Change ##x## to ##x + d##. See what happens.
I should note that this only establishes the ##d## is a period. If you shift a sine wave of period ##T## by 10 periods, you get the same sine wave, so ##10T## is a period but not the smallest period. You have to do a little more reasoning to establish that ##d## is the smallest period.
Mark44
Mentor
- 38,031
- 10,506
Thread closed as the OP has been banned.
Insights auto threads is broken atm, so I'm manually creating these for new Insight articles.
In Dirac’s Principles of Quantum Mechanics published in 1930 he introduced a “convenient notation” he referred to as a “delta function” which he treated as a continuum analog to the discrete Kronecker delta. The Kronecker delta is simply the indexed components of the identity operator in matrix algebra
Source: https://www.physicsforums.com/insights/what-exactly-is-diracs-delta-function/
by...
Fermat's Last Theorem has long been one of the most famous mathematical problems, and is now one of the most famous theorems. It simply states that the equation
$$
a^n+b^n=c^n
$$
has no solutions with positive integers if ##n>2.## It was named after Pierre de Fermat (1607-1665). The problem itself stems from the book Arithmetica by Diophantus of Alexandria. It gained popularity because Fermat noted in his copy
"Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et...
I'm interested to know whether the equation
$$1 = 2 - \frac{1}{2 - \frac{1}{2 - \cdots}}$$
is true or not. It can be shown easily that if the continued fraction converges, it cannot converge to anything else than 1. It seems that if the continued fraction converges, the convergence is very slow. The apparent slowness of the convergence makes it difficult to estimate the presence of true convergence numerically. At the moment I don't know whether this converges or not.
Similar threads
- Replies
- 33
- Views
- 3K
- Replies
- 1
- Views
- 2K
- Replies
- 20
- Views
- 3K
- Replies
- 7
- Views
- 1K
- Replies
- 5
- Views
- 1K
- Replies
- 1
- Views
- 959
- Replies
- 5
- Views
- 1K
- Replies
- 6
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 2
- Views
- 1K
Hot Threads
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
B How is it that law of sines does not work in this exercise?
- Started by mcastillo356
- Replies: 70
- General Math
-
B What could prove this wrong? I'm having a dispute with friends
- Started by ducknumerouno
- Replies: 94
- General Math
-
B About a definition: What is the number of terms of a polynomial P(x)?
- Started by littlemathquark
- Replies: 48
- General Math
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 0
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math