Permanent Magnets: Find Net Force Acting on Assembly

[specificio]

Hello!

I have a deeply magnetizing question. I have an attractive magnetic assembly and I am interested in finding some forces, acting on its parts.

Set-up details ( if to be specific ):

I have two cylinder-shaped neo magnets with identical dimensions and properties, such as residual induction, dimensions, mass, etc.

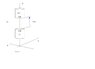
I fix both of 'em as shown in the attachment A1.gif below. M1 is fixed on the ground, M2 can only move thru Y-axis. M2 is attracted by gravity, but hangs in the air because of the repulsive force between those two.

Target:
I have to find the net force in Newton units, acting on M2, thus it's being fixed in its levitated state and doesn't move. The sticky point is that I want to design a magnet, which will hold another one at certain air gap, but for this purpose a horse, pardon, a force value needed.

What I do know:
I know nothin' about it, as the school project has just begun; this is my first week with permanent magnets. So my questions to you:

• Could you provide me with any ( specific ) guidelines for further reading? Google did not help me a lot in this case.
• or, could you give me some kind of hint for the strategy of calculation, which I should follow?
• How the Magnetic Flux Density ( induction ) of a given magnet does relate to the resulting force?
• I have gotten a link to so-called "magnetic moment" or torque as a force expression, but it just doesn't make sense, I am not sure it's what I need. Is it?

I’m totally lost in this forest. Any help would be appreciated.. ..even if there are no threes.



Lyric notes:
When I’m talking about induction, I visualize the following calculation in my mind: see att. A2.gif
The purpose of this project is to develop ( OK, to try to develop ) a magnetic ( frictionless ) bearing for the windmill. It is interesting to check – will it work or will it not do so.

 

[OlderDan]

This appears to be applicable to your problem

http://en.wikipedia.org/wiki/Magnet

 

[specificio]

All right, thank you for the help, I'll take a look at it.

- - - - - - - - - - - - - - - -
Now I understand..

I've found most of the needed literature, and will make sure not to repeat this kind of mistakes in the future.
Thank you for the right kick!
I.L.

 

[AlephZero]

Magnetic bearings certainly exist. They are usually called "Active Magnetic Bearings" or AMB's. See http://en.wikipedia.org/wiki/Magnetic_bearing

 

[specificio]

Magnetic bearings certainly exist. They are usually called "Active Magnetic Bearings" or AMB's. See http://en.wikipedia.org/wiki/Magnetic_bearing

Thank you, A. Zero.
It is a very good information to start with. My current point of view is, that AMB's need an energy source, and therefore they are likely not to become useful in a windmill, because it is a bit risky and can cost a lot, if it fails.

I'm trying to find out, what a PMB*[1] might be able to do. There is a tricky problem of fixed magnetic configuration, and some calculations have to be performed on this basis. So I am searching for the basic "rules" for the game, so to speak, because I am startin' from the beginning.

What our group wants to do - is to allow a windmill to start at lower wind speeds due to reduced energy loss by using a frictionless PMB assembly, and if we can't build it, we will model it. Inspiration came from energybulletin.net, or more precise, from http://www.worldwatch.org/node/4217" - the difference is, that we want to build and test our own.I.L.

*[1] Passive Magnetic Bearing.