Reverberant
- 2
- 0
Hello,
I'm taking my first calculus course right now, and something struck me regarding the remainder in integral form of a Taylor series expansion:
Let's say we have a Taylor expansion of the (n-1):th order, which has a remainder of the form
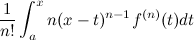
Now, my claim is that if we integrate by parts n-1 times (I think), then every term of the integrated remainder, except for the last one, will cancel out a term of the Taylor polynomial; leaving only f(x). Thus, all we have left is the equation f(x)=f(x).
Is this true, and if so, can you confirm that the form of integration by parts to be used is
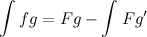
and not
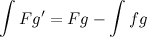
?
Thanks in advance!
I'm taking my first calculus course right now, and something struck me regarding the remainder in integral form of a Taylor series expansion:
Let's say we have a Taylor expansion of the (n-1):th order, which has a remainder of the form
Now, my claim is that if we integrate by parts n-1 times (I think), then every term of the integrated remainder, except for the last one, will cancel out a term of the Taylor polynomial; leaving only f(x). Thus, all we have left is the equation f(x)=f(x).
Is this true, and if so, can you confirm that the form of integration by parts to be used is
and not
?
Thanks in advance!