Perturbation theory infinite well

[Dammes]

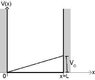
in the infinite well with small potential shown in the attachment.
I calculated the total energy by using the time independent Schrodinger equation and adding the correction energy to the equation of the slope k=(Vo/L)x.

E=h^2/8mL^2 +∫ ψkψ dx

ψ=√(2/L) sin⁡(∏/L x)

when integrating ∫ ψkψ dx between 0 and L
I got Zero, ∫ ψkψ dx=0
∴ total energy=h^2/8mL^2 +0

so what i don't understand is when adding a small potential it doesn't affect the total energy of the system? that is what it shows when i integrated it.

 

[TSny]

i
when integrating ∫ ψkψ dx between 0 and L
I got Zero, ∫ ψkψ dx=0

I don't believe that integral is zero. Check your work to see if you might have made a mistake.

 

[Dammes]

i have looked over and did it again, i still get zero.
could you please try out the integral
∫ ψkψ dx

where ψ=√(2/L) sin⁡((∏/L) x)
and
k=(Vo/L)x

 

[TSny]

Maybe you can show some of the steps of how you integrated \int_0^L sin^2(\pi x/L)\; x \;dx. Note that the integrand is positive throughout the range of integration. So, it's got to yield a positive result.

 

[Dammes]

the pictures in the attachment shows some of my working

 

[Dammes]

looking over it again i see where i went wrong, i used integration in the product rule. sorry for wasting your time and thank you very much!

 

[Dammes]

sorry, please don't read my previous comment. i see where i acutely went wrong, i have to use integration by parts. i have a problem of mixing up integration and differentiation.
hope I am correct this time
sorry and thank you

 

[TSny]

No need to be sorry. Glad to be of help.