The phase velocity manifests as a general spreading of the water wave.
You'll be able to see it more clearly when there's a pulse instead of a wave-train.
http://www.acs.psu.edu/drussell/Demos/Dispersion/dispersion.html
OTOH: you do get varying amplitude waves coming at you in water.
Dispersion is where the characteristic length of a
pulse increases as it propagates.
You seem to be thinking of all waves as having a definite wavelength ... like a sine wave does.
This is incorrect.
A water wave, or any wave for that matter, is
any solution to the wave equation.
Sine waves are solutions to the wave equation, but they are not the only solutions.
General solutions to the wave equation can be expressed as linear sums of pure sine waves.
A pure sine wave has a specific wavelength and wave speed - the wave speed depends on the medium, and, in a "dispersive medium" the wave speed depends on the wavelength.
A pure sine wave is the only kind of wave which can be characterized by having a specific, single, wavelength.
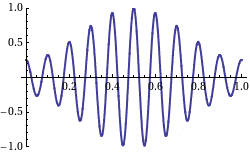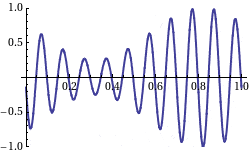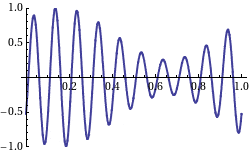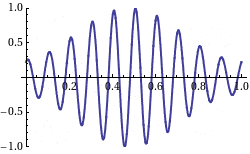
The waves in your example, for instance, exhibit two clear wavelengths and would be typically composed of around 100 individual sine waves.
The wavelength of a pure sine wave does not change as it propagates.
A general wave cannot be characterized by having a single wavelength - but it can be characterized by the mixture of pure sine waves that make up it's overall shape.
Since these sine waves will each travel at a different speed, the overall shape of the wave will change st it propagates. The overall shape of a general wave is a transient.
The dispersion relations tell you how the shape changes.
The examples, like the ones you've seen in animations, are for simple situations where the math is not too hard and it is easier to see specific effects.
A real life wave in Nature (take a close look at the surface of the sea sometime) tends to be very complicated and it is harder to see particular effects.
That is why you do not generally associate the shape in post #1 with water waves.
But you will see wave-trains like that in the wakes of boats - you have to look carefully.
You'll notice that the wave in your example does not change it's overall shape so much - this is because a lot of small changes cancel out to an overall impression of a wiggly shape moving. This is an emergent phenomenon - what is happening is that lots of sine waves are moving at different speeds and they interfere constructively and destructively with each other.
So - in general - dispersion is the emergent phenomenon arising from the components of waves and pulses moving at different speeds through the same media.