A Physical significance of growth rate in plasma

sreerajt
Messages
39
Reaction score
1
Let us say that we have a dispersion relation curve and associated instability curve as shown below for a magnetised plasma, which have been formulated through kinetic theory. The frequencies and growth rate have been normalized w.r.t. cyclotron frequency of proton.
test.jpg
My question is: what does this both plot physically signifies?
 

Attachments

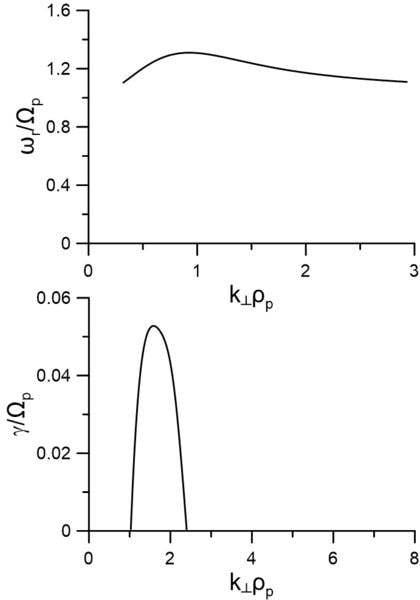  • test.jpg
    test.jpg
    12.6 KB · Views: 394
  • test.jpg
    test.jpg
    12.6 KB · Views: 804
Physics news on Phys.org
sreerajt said:
......
My question is: what does this both plot physically signifies?
You have marked your thread with an "A" tag signifying post graduate level ...
So what study / readings have you been doing so far ... show some links
show us what parts of them that you do not understand so that people here might
be able to help you
 
davenn said:
You have marked your thread with an "A" tag signifying post graduate level ...
So what study / readings have you been doing so far ... show some links
show us what parts of them that you do not understand so that people here might
be able to help you
This kind of graph appears at many places where one invoke kinetic theory to study plasma. E.g. kindly see research article at:
  1. https://www.cambridge.org/core/jour...-instability/86419F5E132B4437D6DDAD0469179B6C
  2. https://www.cambridge.org/core/jour...e-ion-plasma/2685E71532119D417D1C6B8E1FE23FD7
 

Thread 'Toponium Discovered'

Toponium is a hadron which is the bound state of a valance top quark and a valance antitop quark. Oversimplified presentations often state that top quarks don't form hadrons, because they decay to bottom quarks extremely rapidly after they are created, leaving no time to form a hadron. And, the vast majority of the time, this is true. But, the lifetime of a top quark is only an average lifetime. Sometimes it decays faster and sometimes it decays slower. In the highly improbable case that...
View full post »

Thread 'Dirac-Delta from Normalization of Continuous Eigenfunctions'

I'm following this paper by Kitaev on SL(2,R) representations and I'm having a problem in the normalization of the continuous eigenfunctions (eqs. (67)-(70)), which satisfy \langle f_s | f_{s'} \rangle = \int_{0}^{1} \frac{2}{(1-u)^2} f_s(u)^* f_{s'}(u) \, du. \tag{67} The singular contribution of the integral arises at the endpoint u=1 of the integral, and in the limit u \to 1, the function f_s(u) takes on the form f_s(u) \approx a_s (1-u)^{1/2 + i s} + a_s^* (1-u)^{1/2 - i s}. \tag{70}...
View full post »

Similar threads

Plasma thruster - plasma instability in magnetic nozzle
Replies
0
Views
2K
Studying Preparing for Plasma Physics (Jackson)
Replies
4
Views
3K
How to determine the minimum grid length | Numerical Plasma Physics
Replies
7
Views
2K
B What Is the Physical Significance of Logarithmic IV Graphs in Diodes?
Replies
3
Views
4K
I Does the New Muon g-2 Measurement Indicate Physics Beyond the Standard Model?
Replies
2
Views
2K
Phase-space structures in plasma turbulence
Replies
2
Views
3K
  • Poll Poll
Astrophysics Physics Of Space Plasmas: An Introduction, 2nd Ed, by George Parks
Replies
1
Views
5K
B Is information the 5th state of matter?
Replies
18
Views
3K
I How powerful would a collider have to be to observe a sphaleron?
Replies
2
Views
3K
Programs Physics Minor - Course Selection for ME
Replies
6
Views
2K

Hot Threads

Recent Insights

Back
Top