Physics Forces Question with mass

[Hannahj1]

Homework Statement

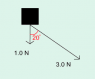
A force of 3.0 N and 1.0 N act on a 6.0 kg mass as shown. What is the acceleration of the 6.0 kg mass?

Homework Equations

Fnet = ma

The Attempt at a Solution

I did 3N as fnet so fnet=ma, 3=6a and solved for a
i was just wondering if what i did was right and if i need to incorporate the 1N in any way? Thank you

 

[TSny]

Hi, Hannahj1.

Can you give a reason for neglecting the 1.0 N force when finding the net force?

 

[Hannahj1]

Hi, Hannahj1.

Can you give a reason for neglecting the 1.0 N force when finding the net force?

When you find the net force it is usually the hypotenuse of the x and y components and here you're already given the hypotenuse (the 3N)

 

[laplacean]

Yes, you do need to incorporate the 1N. Vector addition is necessary in this problem, as both forces have components that contribute to the acceleration of the block. You cannot ignore the 1N.

 

[haruspex]

When you find the net force it is usually the hypotenuse of the x and y components and here you're already given the hypotenuse (the 3N)

That's because you are used to being given problems in which the applied forces are at right angles to each other, so the resultant is the hypotenuse.
But in general, as here, the applied forces can be at any angle to each other. The 3N line is not the hypotenuse of any triangle of interest.

A standard technique is to pick a pair of directions at right angles (vertical and horizontal in the screen shot would be convenient) and resolve each applied force into components in those two directions. Then you can add the components in each direction separately, and finally figure out what the resultant of those two forces is. Here, at last, you will be looking for the hypotenuse.
Do you know how to resolve a force into its components?