Bdb1331
- 2
- 0
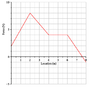
The diagram shows how a force along the x-axis varies with location. A block of mass 7.20 kg moves along the x-axis on a horizontal frictionless surface, influenced by this force. (Graph is attached)
A) How much work is done by the force as the block moves from the origin to 8.0 m?
B) If the block has a velocity of 3.80 m/s at the origin, what is its velocity at 8.0 m?
For part A, I worked out the work to be 33 J by finding the area under the curve...
in the first two seconds
W = F(avg)d
W = [(2 + 8) / 2](2 - 0)
W = 10 J
from 2 to 4 seconds
W = [(8 + 4)/2] (4 - 2)
W = 12 J
from 4 to 6 s
W = 4(6 - 4)
W = 8 J
from 6 to 8 s
W = [(4 + -1)/2](8 - 6)
W = 3 J
Total work
W = 10 + 12 + 8 + 3
W = 33 J
But I am sort of lost when it comes to B)
A) How much work is done by the force as the block moves from the origin to 8.0 m?
B) If the block has a velocity of 3.80 m/s at the origin, what is its velocity at 8.0 m?
For part A, I worked out the work to be 33 J by finding the area under the curve...
in the first two seconds
W = F(avg)d
W = [(2 + 8) / 2](2 - 0)
W = 10 J
from 2 to 4 seconds
W = [(8 + 4)/2] (4 - 2)
W = 12 J
from 4 to 6 s
W = 4(6 - 4)
W = 8 J
from 6 to 8 s
W = [(4 + -1)/2](8 - 6)
W = 3 J
Total work
W = 10 + 12 + 8 + 3
W = 33 J
But I am sort of lost when it comes to B)