yungman
- 5,741
- 294
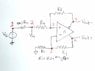
I am having a very difficult time verifying the equations for full differential amplifier. I literally read all the articles I can find from Google. Here is one of the question I think the paper by Jim Karki is wrong. The equation is equation (9). I verified the rest of the equation already, only the (9) is wrong. But I want to verify this here first. This is the paper I am referring to:
http://www.ti.com/lit/an/slyt310/slyt310.pdf
http://www.ti.com/lit/an/slyt310/slyt310.pdf
This is my work to proof the article is wrong.

I go step by step using Thevenin to get the gain of VOD/VSIG is what the paper claim is VOD/VIN. Please help me verifying.
Thanks
http://www.ti.com/lit/an/slyt310/slyt310.pdf
http://www.ti.com/lit/an/slyt310/slyt310.pdf
This is my work to proof the article is wrong.
I go step by step using Thevenin to get the gain of VOD/VSIG is what the paper claim is VOD/VIN. Please help me verifying.
Thanks