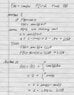barryj
- 856
- 51
- Homework Statement
- I have this problem and solution. I do not understand the solution, in particular how the integral fits into the solution. Is this a form of the 2nd theorem of calculus perhaps? I am confused.
if f'(x) = cos (x^3) and f(1) = 2 find f(0)
- Relevant Equations
- I have attached the problem statement and he solution.
f(x) = sin(x) + C and then evaluate C by knowing that 2 = sin(1) + C and then C would equal 2-sin(1)
the f(x) = sin(x) + 2 - sin(1),
f(0) = sin(0) + 2 - sin(1) = 0 + 2 -.841 = 1.58
However the more complicated problem has f'(x) - cos(x^3) and it is solved using an integral expression that is evaluated with a calculator.
I do not understand this integral method. Please help or point me to a link where I can find out what is going on.
Last edited by a moderator: