Find the Angle of a Sliding Solid on a Ball: Step-by-Step Guide

[mohlam12]

okay here is the scenario
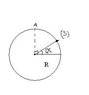
you have a ball (radius R) and above that ball, there is a solid S that has a mass M and it is on a point A of the ball. You slightly push that solid and it slides around the ball then it leaves the ball at an angle ALPHA. you have to find that angle.
You only have that g=9.81m/ss and that s all.

here is a little drawing...

Please i really need it as soon as possible. thanks

 

[Doc Al]

Show us what you've done so far and where you are stuck.

 

[mohlam12]

okay
well i used the theorem where you have all the forces equal to the vector of acceleration by the mass... you have the two forces P, and R which is the force coming from the surface of the ball. when the solid leaves the ball, R is equal to zero... but I didnt get to anything.

I used the conservation of mechanic energy in two points, A and B (where the solid quits the ball) I didnt get to anything neither.

if you can just give me hints of what to use or where to start.. thank you

 

[Doc Al]

okay
well i used the theorem where you have all the forces equal to the vector of acceleration by the mass... you have the two forces P, and R which is the force coming from the surface of the ball. when the solid leaves the ball, R is equal to zero... but I didnt get to anything.

If you are attempting to apply Newton's 2nd law, then you are on the right track. What forces act on the mass at any given distance (or angle) from the top? Hint: How is the mass accelerating?

I used the conservation of mechanic energy in two points, A and B (where the solid quits the ball) I didnt get to anything neither.

Conservation of energy is also important for this problem. What's the kinetic energy of the mass after it reaches a given angle?

Newton's 2nd law and conservation of energy are the two things you need to solve this problem. Keep going!

 

[arildno]

Well, think of the following:
Why is the point mass able to follow the curved surface in the first place?
EDIT:
Dear, oh dear, too late..

 

[mohlam12]

There is the weight P and the surface of the ball R. What makes the mass accelerating is that one force is bigger than the other. The force P changes when the angle change because it equals mgsinALPHA... and the R, I don't know.
When it reaches a give angle, the kinetic energy is equal to 0.5mv² that doesn't have anything to do with a given angle...

 

[arildno]

What sort of acceleration must an object have if its trajectory is curved?

 

[mohlam12]

When we project the two forces on Frenet plot we get
R - mg cos(alpha) = m(v²/radius)
mg sin (alpha) = ma

don't really know what to do next, i have no a, nor the radius, nor R nor anything...

 

[Doc Al]

There is the weight P and the surface of the ball R. What makes the mass accelerating is that one force is bigger than the other. The force P changes when the angle change because it equals mgsinALPHA... and the R, I don't know.

Draw a diagram of the mass when it's at some angle alpha. Show the forces acting on it--both radially and tangentially. What can you say about the acceleration as it slides along the surface? Hint: Pay particular attention to the radial direction.

When it reaches a give angle, the kinetic energy is equal to 0.5mv² that doesn't have anything to do with a given angle...

The kinetic energy equals 0.5mv^2 at any angle--by definition. You need to find the kinetic energy as a function of alpha. Use conservation of energy.

 

[mohlam12]

Okay.. I found using the conservation of energy that the kinetic energy is equals to 0.5r(R- gcos(alpha)/m)
I also found that
g(1-sin alpha)=0.5 R/m - gcos alpha

EDIT
for the radial forces, there is : R-mgcos alpha = mv²/r

 

[mohlam12]

Please I am Lost Help !

 

[mohlam12]

It s midnight and my head hurts SO bad and i ve been working on it since 3 hours and i refuse to go to bed til i find the answer. would someone just start it to me ! I REALLY need to solve it!

OK... finally i came out to

(cos alpha)/2 - sin alpha = R/2gm - 1

 

[Doc Al]

Okay.. I found using the conservation of energy that the kinetic energy is equals to 0.5r(R- gcos(alpha)/m)
I also found that
g(1-sin alpha)=0.5 R/m - gcos alpha

Well... the change in potential energy is:
$$mg\Delta h$$
So the kinetic energy must equal:
$$mgR(1 - \sin\alpha)$$

(where R means radius)

EDIT
for the radial forces, there is : R-mgcos alpha = mv²/r

Almost. Realize that the centripetal acceleration acts toward the center, and that the radial component of the weight is:
$$mg \sin \alpha$$

(Use a different letter than "R" to represent the normal force, otherwise you'll confuse it with the radius.)

Don't stop now.

 

[mohlam12]

Got it...
Thanks everyone