- #1
Saladsamurai
- 3,020
- 7
PLEASE! Shear Flow HELP
We are doing shear flow problems and my instructor has been unable to explain the topic in a general enough way to apply effectively to all problems. Our (my class) difficulty is understanding in the formula q=QV/I where the variable Q=yA' what to use for A'.
It seems to vary so drastically from problem to problem that there is no set way to find it.
Will someone please explain to me what to use for A' in this problem:
The three boards are nailed together as shown. How should the nails be spaced if each nail can resist 100 lbs?
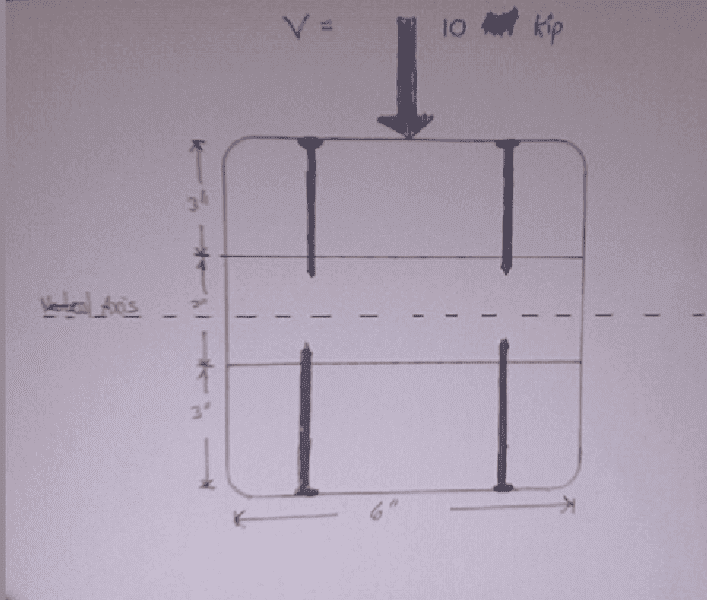
I was thinking of using [tex]q=\frac{F}{spacing}=\frac{QV}{I}[/tex] and only using the area of the top board. This would get me the spacing if there were only two nails. Then I could multiply that number by two to get it for four nails since it is symmetrical about the neutral axis.
Does this sound right?
We are doing shear flow problems and my instructor has been unable to explain the topic in a general enough way to apply effectively to all problems. Our (my class) difficulty is understanding in the formula q=QV/I where the variable Q=yA' what to use for A'.
It seems to vary so drastically from problem to problem that there is no set way to find it.
Will someone please explain to me what to use for A' in this problem:
The three boards are nailed together as shown. How should the nails be spaced if each nail can resist 100 lbs?
I was thinking of using [tex]q=\frac{F}{spacing}=\frac{QV}{I}[/tex] and only using the area of the top board. This would get me the spacing if there were only two nails. Then I could multiply that number by two to get it for four nails since it is symmetrical about the neutral axis.
Does this sound right?