binbagsss
- 1,291
- 12
Homework Statement
I have ##C= NK_B (\frac{\epsilon}{K_B T})^{2}e^{\frac{\epsilon}{K_B T}}\frac{1}{(e^{\frac{\epsilon}{K_BT}}+1)^2} ##
and need to sketch ##C## vs. ##T##
Homework Equations
See above
The Attempt at a Solution
I have ##C= NK_B (\frac{\epsilon}{K_B T})^{2}e^{\frac{\epsilon}{K_B T}}\frac{1}{(e^{\frac{\epsilon}{K_BT}}+1)^2} ##
Considering asymptotic limits I have:
##C \to e^{-\frac{\epsilon}{K_{B}T}} ## as ##T \to 0##
##C \to \frac{1}{T^{2}} ## as ##T \to \infty##
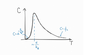
The solution is attached.
So from these limits I get the shape at these ends, and deduce there is a maximum to allow me to sketch the rest of it.
I am unsure how to deduce this maximum?
Differentiating gives quite a mess and it seems that it should be obvious to conclude the maximum is at ## \epsilon / K_{B} ##, or at least a better method to find this point? (My knowledge of graph sketching is quite poor).
Many thanks in advance.
Attachments
Last edited: