Rod Alexei
- 29
- 0
1. Homework Statement
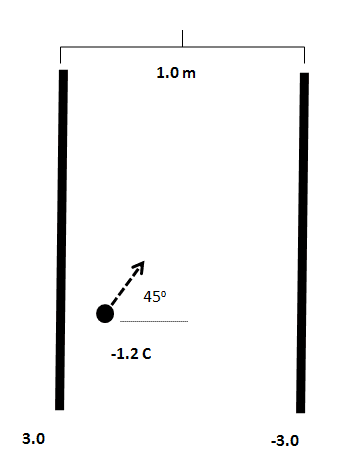
A fixed parallel plate capacitor is charged. A point charge is starting to move with an initial speed 1.0 m/s at shown initial position. The capacitance is 5.0 F. The mass of the point charge is 0.80 kg. Assume that the plate length is infinite. No gravity. The initial distance between the charge and the positive plate is 0.3 m. The charges of the two plates are 3 C and -3C.
(a) What is the potential difference between the two plates?
(b) Draw the trajectory of the point charge on the figure given below.
(c) Find the nearest distance between the point charge and the negatively charged plate during motion.
(d) Find the largest speed of the point charge during the motion.
(a) /_\ (delta) v = Q/C= 3/5 = 0.6 V
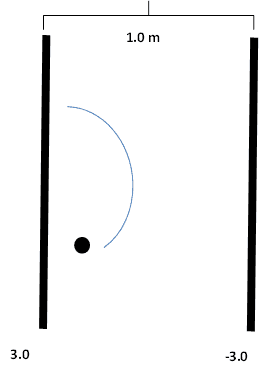
(b)
(c) W= /_\K
I do not know what to do next.
(d) I also do not know where to begin.
A fixed parallel plate capacitor is charged. A point charge is starting to move with an initial speed 1.0 m/s at shown initial position. The capacitance is 5.0 F. The mass of the point charge is 0.80 kg. Assume that the plate length is infinite. No gravity. The initial distance between the charge and the positive plate is 0.3 m. The charges of the two plates are 3 C and -3C.
Homework Equations
(a) What is the potential difference between the two plates?
(b) Draw the trajectory of the point charge on the figure given below.
(c) Find the nearest distance between the point charge and the negatively charged plate during motion.
(d) Find the largest speed of the point charge during the motion.
The Attempt at a Solution
(a) /_\ (delta) v = Q/C= 3/5 = 0.6 V
(b)
(c) W= /_\K
I do not know what to do next.
(d) I also do not know where to begin.
Last edited: