Pole in a corner - Trig word problem

[MacLaddy]

Homework Statement

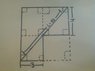
A pole of length L is carried horizontally around a corner where a 3-ft wide hallway meets a 4-ft wide hallway. For $0 < \theta < \frac{\pi}{2}$, find the relationship between L and $\theta$ at the moment when the pole simultaneously touches both walls and the corner P. Estimate $\theta$ when L = 10 ft.

Please see picture for representation

Homework Equations

Pythagorean Theorem

The Attempt at a Solution

I don't know. Take a look at the picture of the workup I did on my white board. I just can't seem to make a connection here. I feel like I am going to need to make 3 of some variable equal 4 of some variable, but I could be completely off.

I don't believe I have enough information to apply the Law of Sines/Cosines.

Any help would be appreciated.

Mac

 

[genericusrnme]

oh man, that first image made me laugh

I'm just about to go to sleep so I might be wrong about this (I haven't gone through with the whole thing in my head yet) but what I'd try and do would be to solve for one of the lengths of the bottom right box. You could then find the lengths of each side of the plank, if you want to try this route then use pythagoras but think of the larger triangle rather than the two smaller ones

if you've already tried this then I dunno..
if you've not already solved this I'll try and come back tomorrow if I am not too busy :D

 

[Benn]

uploaded an explanation.. <33 white boards

http://i44.tinypic.com/sy5zrn.jpg

I'm assuming that the corner is a right angle (which, I think, is a pretty fair assumption.)

 

[MacLaddy]

Thanks for the explanation, Benn.

I follow your solution all the way through $sin(90-\theta)=cos\theta= \frac{3}{x}$ That is the sly key that I was missing. You lose me however when you post x=y, and down from there. That's okay though, you gave me the start I needed to finish the triangle.

If the sin and cos equal each other on the bottom triangle, then the bottom triangle has sides x=3, y=3, and r=$\sqrt{18}$, and the top triangle has sides x=4.14, y=4, and r=5.76

These number also jive if you make one large triangle out of the two. I'll finish examining the angles tomorrow morning.

Thanks again, and I would greatly appreciate it if someone could verify what I'm saying just to check my work. (it is very late here now)

Mac

 

[Benn]

http://i43.tinypic.com/1z3qsly.jpg

I hope this helps.

 

[MacLaddy]

Thanks again, Benn.

I think the only thing I am confused on is how are you sure that x=y, and that the denominators describe the hypotenuse of the same angle? I could see that being the case if we were sure that the overall length of the pole was touching right in the middle. I know that x+y = 10, but couldn't it be x=7, y=3, or any other variant? ( I know it has to be something exact, but I'm just using an example)

If you could clarify on that part I would appreciate it. I'm sure that I am missing something obvious here so I apologize for being a bit sluggish in the brainskills.

 

[MacLaddy]

Just to add a thought. If both triangles are 3-4-5 as you suggest then this is probably where I am making a mistake, so maybe you can point it out in my reasoning below.

Let's call the top triangle TR1, and the bottom TR2. If the angle of TR1 is $sin\theta$, and the angle of TR2 is $sin(90-\theta)=\frac{3}{x}$, then with the shown identity doesn't the cosine also equal $\frac{3}{x}$?

If what I said above is true, then that would give the two sides of TR2 3 and 3, with a hypotenuse of $\sqrt{18}$

 

[MacLaddy]

I hope I don't come across as ungrateful or impatient, as I do appreciate the assistance above, but I really could use some double-checking on this problem.

If someone would be willing to just point out the error of my ways my life would be completely fulfilled. (until the next problem, that is)

 

[SammyS]

The posts in this thread would be much more readable if the images were posted directly with the text, rather than in links or thumbnails.

Images from thumbnails in OP:

Image from Post #2, Benn's white board:

Image from Post #4, by Benn:

 

[SammyS]

Thanks again, Benn.

I think the only thing I am confused on is how are you sure that x=y, and that the denominators describe the hypotenuse of the same angle? I could see that being the case if we were sure that the overall length of the pole was touching right in the middle. I know that x+y = 10, but couldn't it be x=7, y=3, or any other variant? ( I know it has to be something exact, but I'm just using an example)

If you could clarify on that part I would appreciate it. I'm sure that I am missing something obvious here so I apologize for being a bit sluggish in the brain skills.

Hello MacLaddy.

You are correct in being skeptical regarding Benn's insistence that x = y, where x is the length of the pole in the 3 ft wide hall and y is the length of the pole in the 4 ft wide hall. While it is true that the pole will fit in the junction of the hallways in that configuration, that is as far as you could get if the pole was being carried from the 3 ft hallway to the 4 ft hallway -- the opposite direction from what is asked in this problem.

I don't particularly like those choices of names for the variables, since x is often a horizontal distance & y a vertical distance.

Let L₃ be the distance from the corner to the point at which the pole contacts the wall in the 3 ft hall and similarly, L₄ be the distance from the corner to the point at which the pole contacts the wall in the 4 ft hall.

Suppose that L₃ = 4.5 ft. It can be shown that a 10 ft long pole will not fit in the junction of these two hallways in either of the following two ways.

1. By finding that L₄ < 5.5 ft. if the hallways are of the stated width. (This gives L < 10 ft.)

2. Assuming that L₄ = 5.5 ft (so that L = 10 ft) and the destination hallway is 3 ft wide, it can be shown that the first hallway needs to be more than 4 ft in width.
​

 

[HallsofIvy]

Isn't there a "sticky" for this problem? We've seen it many times.

 

[MacLaddy]

Thank you for the reply, SammyS.

If you see my posts 4 & 7 above you can see that I offered a solution to this problem. I would retype it but I am currently using my cell phone.

Following your reasoning I would suspect my answer is correct, but that is what I am hoping someone will double check.

Thanks again,
Mac

 

[SammyS]

MacLaddy see HallsofIvy's post above.

From Post #4:

...

If the sin and cos equal each other on the bottom triangle, then the bottom triangle has sides x=3, y=3, and r=$\sqrt{18}$, and the top triangle has sides x=4.14, y=4, and r=5.76

These number also jive if you make one large triangle out of the two. I'll finish examining the angles tomorrow morning.

Thanks again, and I would greatly appreciate it if someone could verify what I'm saying just to check my work. (it is very late here now)

Mac

The x & y in the top triangle should also match each other.

This isn't actually a solution, but at θ = 45° the largest L can be is about 9.8995 ft.

From Post #7:

Just to add a thought. If both triangles are 3-4-5 as you suggest then this is probably where I am making a mistake, so maybe you can point it out in my reasoning below.

Let's call the top triangle TR1, and the bottom TR2. If the sine of the angle of TR1 is $sin\theta$, and the sine of the angle of TR2 is $sin(90-\theta)=\frac{3}{x}$, then with the shown identity doesn't the cosine also equal $\frac{3}{x}$?

If what I said above is true, then that would give the two sides of TR2 3 and 3, with a hypotenuse of $\sqrt{18}$

Thank you for the reply, SammyS.

If you see my posts 4 & 7 above you can see that I offered a solution to this problem. I would retype it but I am currently using my cell phone.

Following your reasoning I would suspect my answer is correct, but that is what I am hoping someone will double check.

Thanks again,
Mac

Well, those aren't solutions to the problem as it is asked.

You need to

"find the relationship between L and θ at the moment when the pole simultaneously touches both walls and the corner P. Estimate θ when L = 10 ft. "​

You showed that θ can't get to 45° if the pole is 10 ft long.

To find the angle, θ, when the pole first contacts both walls & the corner, you either have to use calculus or use a graphing calculator.

 

[SMcM]

Several months late, but maybe helpful to someone else. I couldn't find much help on this problem, but then I finally figured it out. Using the diagrams and work already posted we see that x = 3/cos(θ) and y = 4/sin(θ). However, x + y = L. So, this leads to the desired relationship between L and θ. (There is no need to assume a 3-4-5 or that x = y.)

As far as I can tell, to solve for θ when L = 10 requires a CAS or guess & check with a scientific calculator.