6Stang7
- 212
- 0
I've been working on this problem and I cannot find out where I am making a mistake.
Two charges, each with a value of +q, are placed a distance d apart on the x-axis. Find the potential at a point P a distance z above the x-axis on the z-axis
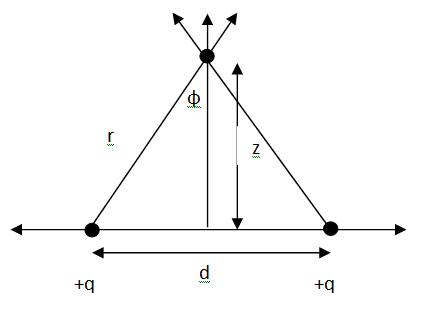
The figure below shows the physics system:
The potential due to a charge is given by:
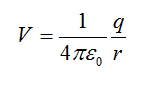
We can express r as:
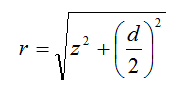
We can see by symmetry that the x-components will cancel out, so the total potential will be twice of the z-component. The z-component of the potential is the cosine of the magnitude, where cosine is:
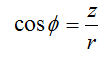
This gives us:
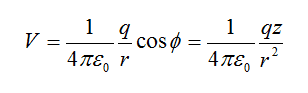
Putting everything together we get:
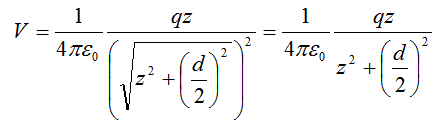
Therefore, the total potential at point P is:

Now, we know that the potential is related to the Electric Field by:
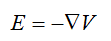
This means that the Electric Field at the same point is (I realize the forget the minus sign just now):
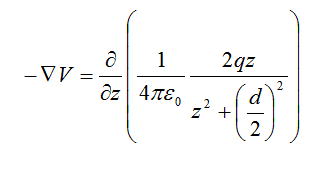
Which when solved give:
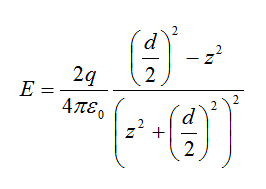
Now, using the same figure, but instead of solving for the potential, we solve for the Electric Field, we find:
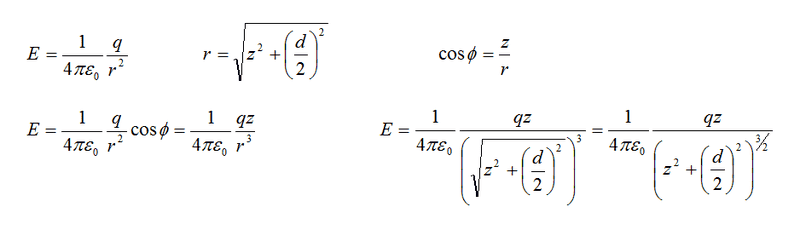
The above uses the same line of thinking, and this gives a total value of the Electric Field to be:
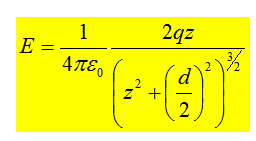
The problem is that the book says that the potential I calculated above is wrong, and that the value should be:

When you calculate the value of the Electric Field from this, you get the same answer as the value I just calculated.
So, what did I do wrong in my calculation of the potential? The error seems to steam from the part where I calculated the z-component of one of the charges using cosine, but I can't see why that is incorrect.
Homework Statement
Two charges, each with a value of +q, are placed a distance d apart on the x-axis. Find the potential at a point P a distance z above the x-axis on the z-axis
The Attempt at a Solution
The figure below shows the physics system:
The potential due to a charge is given by:
We can express r as:
We can see by symmetry that the x-components will cancel out, so the total potential will be twice of the z-component. The z-component of the potential is the cosine of the magnitude, where cosine is:
This gives us:
Putting everything together we get:
Therefore, the total potential at point P is:
Now, we know that the potential is related to the Electric Field by:
This means that the Electric Field at the same point is (I realize the forget the minus sign just now):
Which when solved give:
Now, using the same figure, but instead of solving for the potential, we solve for the Electric Field, we find:
The above uses the same line of thinking, and this gives a total value of the Electric Field to be:
The problem is that the book says that the potential I calculated above is wrong, and that the value should be:
When you calculate the value of the Electric Field from this, you get the same answer as the value I just calculated.
So, what did I do wrong in my calculation of the potential? The error seems to steam from the part where I calculated the z-component of one of the charges using cosine, but I can't see why that is incorrect.