Strange this thread should resurrect itself just as I'm watching another thread about more or less the same issue. I was preparing a post for that making a 'good old fashioned' water analogy! Perhaps I can offer it here for your diversion.
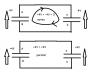
Imagine (because I haven't drawn the diagrams yet!) two tanks for containing liquid: for simplicity let's say they are right prisms (such as a cuboid or a cylinder,) standing on a level plane, with a pipe (of negligible size) connected to the base.
Start with one full of liquid and the other empty, then join the two tanks with a small pipe and let the water flow. The flow will end when the level is equal in both tanks and, if the tanks are the same size, the depth will be half the original depth of the full tank. The pressure at the base of the tanks will obviously be half the original pressure. But as for the potential energy of the water, this will be halved. The total mass of water is the same, but its depth is halved. Half the energy has been dissipated in turbulence.
If the volume of liquid in a tank is v and the area of the tank (base) is A
Pressure is proportional to the depth of liquid in the tank, ##P = ρgh. = \frac{ρgv}{A}## or ## v\frac{ρg}{A}## [Cf ##V= \frac{Q}{C}## ]
[So ##\frac{ A}{ρg}## would be the analogue of C]
PE is proportional to half the height, E= weight * height of CG =## ρgv\times \frac{h}{2} = \frac{v^2 ρg}{2A}## [ Cf ##E= \frac{Q^2}{2C} ## ]
Or ##E= vρg\times \frac{h}{2} = \frac{Pv}{2}\ \ \ ## [ Cf ##E = \frac{VQ}{2}## ]
Or ##E= \frac{Pv}{2} = \frac{PAh}{2} = \frac{P^2A}{2ρg}\ \ \ ## [ Cf ## E= \frac{V^2 C}{2}## ]
So for the two equal tanks, one filled with V volume of liquid,
Initial PE = V2 ρg / 2A
Final PE = 2 x (V/2)2 ρg / 2A = V2 ρg / 4A
If we don't have equal tanks, say the second tank is half the area of the first (full) tank, equilibrium will be reached when a third of the volume has been transferred. The second tank then has half the volume of the first, but both have the same depth = 2/3 of the original depth.
Initial PE = V2 ρg / 2A as before
Final PE = (2V/3)2 ρg / 2A + (V/3)2 ρg / A = [ 4/18 + 1/9 ] V2 ρg / A = V2 ρg / 3A
So final energy is 2/3 of initial (matching the C1/(C1 + C2) ratio) and dissipated energy is 1/3 (matching the C2 / (C1 + C2) ratio )
If we fill the second tank from a pump or enormous reservoir so that the input pressure is constant, like charging a capacitor from a battery, the work input is simply the pressure x volume. Of course the back pressure due to the height of water in the second tank is less than this until the second tank has filled to the necessary depth. So the rest of the pressure must be used overcoming resistance to flow: and flow will be higher at the beginning, tapering off as the other tank fills.
When V volume has flowed and pressure has reached P, the PE of the liquid in the tank is now VP/2 (from the second line of PE expressions above.)
As with the capacitor being charged from a battery, as everyone has said, half the energy supplied is lost. (Here in turbulence and heat, or maybe radiated as sound?)
Of course the proportion of energy lost is tiny, because the reservoir (or C1) is very much larger than the tank (C2)
I don't claim this proves anything, just maybe people struggling with capacitors and their invisible energy, might find tangible water more understandable. For me they key point is to realize that the CG of the water rises at half the rate that the surface level rises.