Ware182
- 7
- 0
Hi,
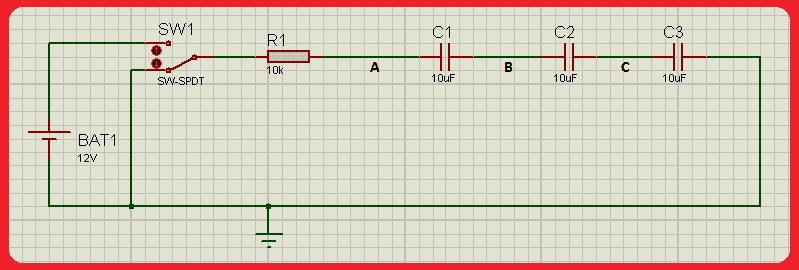
I'm having a problem with this circuit finding potential difference between capacitors. I know the answers by playing around on simulation software A=12v B=8v and C=4v however, I am struggling to use the formula provided Vc= (Vt/Ct)*C to find the answers. It works fine in a parallel circuit with components of the same value but I know that series is different.
1. Homework Statement
Using the formula Vc = (Vt / Ct) * C
So far I understand that VC will be A, B, C
Vt is voltage total=12v
Ct is capacitance total 1/ct=1/c1+1/c2+1/c3 =3.3 recurring
vt/ct=3.6
Now I'm struggling to understand what I times 3.6 by to make either 4, 8 and 12 finishing the formula.
Can anyone help me please?
Thanks
I'm having a problem with this circuit finding potential difference between capacitors. I know the answers by playing around on simulation software A=12v B=8v and C=4v however, I am struggling to use the formula provided Vc= (Vt/Ct)*C to find the answers. It works fine in a parallel circuit with components of the same value but I know that series is different.
1. Homework Statement
Using the formula Vc = (Vt / Ct) * C
- Calculate the voltage at A when SW1 is switched to 12V. 12V (v= I x R)
- Calculate the voltage at B when SW1 is switched to 12V. 8V
- Calculate the voltage at C when SW1 is switched to 12V. 4V
So far I understand that VC will be A, B, C
Vt is voltage total=12v
Ct is capacitance total 1/ct=1/c1+1/c2+1/c3 =3.3 recurring
vt/ct=3.6
Now I'm struggling to understand what I times 3.6 by to make either 4, 8 and 12 finishing the formula.
Can anyone help me please?
Thanks