Samanko
- 14
- 3
- Homework Statement
- When three electric dipoles are near each other, they each experience the electric field of the other two, and the three-dipole system has a certain potential energy. Figure shows two arrangenents in which three electric dipoles are side by side. Each dipole has the same magnitude of electric dipole moment, and the spacings between adjacent dipoles are identical. In which arrangrment is the potential energy of the three-dipole system greater?
- Relevant Equations
- U = - p • E
This is a problem from a textbook, and I can't solve it.
I know that the equation of Potential energy of electric dipole. Since the configuration is a little bit complicated. I'm confused applying which electric fields.

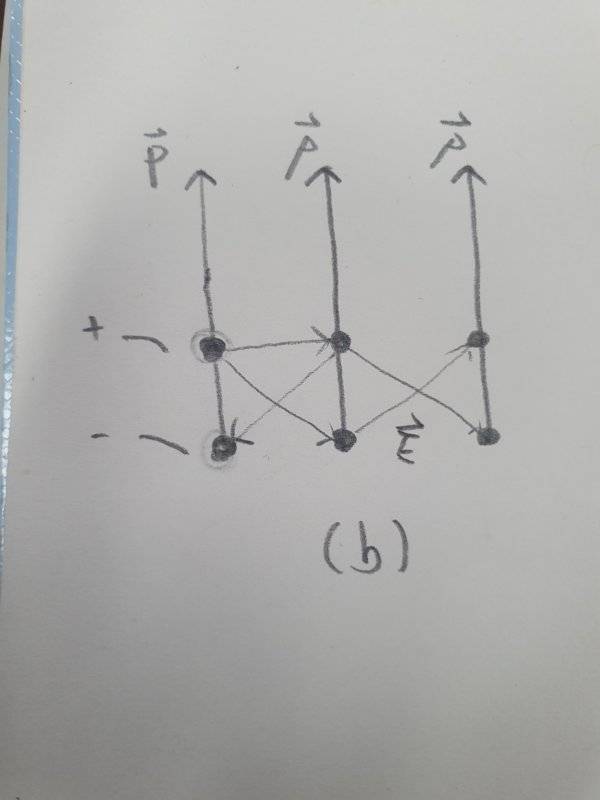
I know that the equation of Potential energy of electric dipole. Since the configuration is a little bit complicated. I'm confused applying which electric fields.