BSJ90
- 8
- 0
Homework Statement
Given that the hemisphere has a charge +Q distributed through its surface with radius a. Find the electric potential on any point on z axis (the plane of the hemisphere is oriented in positive z direction).
Homework Equations
\phi = \int\frac{kQ}{|R-R'|}*ds
(surface integral)
The Attempt at a Solution
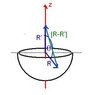
So i decided to break this problem into little pieces of the surface using some trig.
I made a angle θ from the plane of the hemisphere around the cross section (so there is semi circles) and then an angle \varphi on the xy-plane.
I found ds to be a^{2}d\varphid\theta (using the arc lengths of my angles and radii).
Now my problem is finding an equation for the vector R-R'. I tried making it a function of \theta (i.e. i got (sqrt(z^{2} + a^{2}sin^{2}(\theta)
but the integral was not a nice one and it lead me to believe that it wasn't correct. if someone can help me along that would be great!