Potential Energy of Masses on a Pivot

[adkinje]

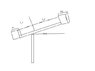
A straight rod of negligable mass is mounted on a frictionless pivot (see attached diagram)Blocks having masses m_1,m_2 are attched to the rod at distances l_1,l_2. (a) Write an expression for teh gravitational potential energy of the blocks-Earth system as a function of the angle \theta made with the horizontal. (b) Find the angle of minimum potential energy. (c) Show that if m_2l_2=m_1l_2 then the system is in equilibrium regardless of the angle \theta

I find that the potential energy function is:

u(\theta)=(m_2l_2-m_1l_1)g_E\sin(\theta)

\frac{du}{d\theta}=(m_2l_2-m_1l_1)g_E\cos(\theta)

Setting the derivative equal to zero gives m_2l_2=m1_l_1.


This seems to address part c. Setting this equal to zero doesn't give an angle (part b). How do I solve part (b)?

 

[adkinje]

I almost forgot the diagram. Attached.

 

[ideasrule]

Use your intuition. If you hold a rod by the middle and attach a mass on one side, at what angle does the rod come to rest?

 

[kuruman]

Setting the derivative equal to zero gives m_2l_2=m1_l_1.

And what happens to your potential energy if this condition is satisfied?