Potential of two points how are they same?

  • Thread starter Thread starter nishantve1
  • Start date Start date
  • Tags Tags
    Points Potential
Click For Summary

Homework Help Overview

The discussion revolves around understanding the concept of electric potential in relation to symmetrical points within a circuit. The original poster expresses confusion about how certain points in a circuit diagram are at the same potential and seeks clarification on the underlying principles.

Discussion Character

  • Conceptual clarification, Assumption checking, Mixed

Approaches and Questions Raised

  • The original poster attempts to understand the reasoning behind points being at the same potential, particularly in relation to symmetrical properties of the circuit. They question the method for identifying points with equal potential and express confusion regarding the application of symmetry in the context of the circuit. Other participants suggest that symmetry plays a crucial role in determining equivalent points and provide examples involving mirror images and symmetry operations.

Discussion Status

Participants are exploring the concept of symmetry in circuits and how it relates to potential differences. Some guidance has been offered regarding the role of symmetry in identifying equivalent points, but the discussion remains open with further questions about specific scenarios and the behavior of current in certain configurations.

Contextual Notes

The original poster mentions a potential reliance on a specific website for additional help, indicating that they are seeking external resources to clarify their understanding. There is also a reference to a specific circuit configuration that may not be fully detailed in the discussion.

nishantve1
Messages
74
Reaction score
1

Homework Statement



I am confused here .
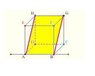
Each wire is of resistance R
How in this image

76xQa.png


E G and D are at the same potential

and in this image
pzhfZ.png

How A and F and Dand G are equivalent?

Homework Equations



I don't think any equations will be used in solving this but I guess V =IR might be

The Attempt at a Solution



In the first image what I figured out is since the points E G and D are at one resistor drop from H so they are at the same potential but I am not able to figure out in the second situation

I am taking help of this website
http://physicstasks.eu/uloha.php?uloha=285
but its quiet confusing
I JUST WANTED TO KNOW WHATS THE METHOD BEHIND FINDING POINTS WITH EQUAL POTENTIAL IN SUCH CASES ?
 
Last edited:
Physics news on Phys.org
Symmetrically equivalent points are at equal potential. Those points are equivalent which transform into each other during a symmetry operation.
Have you got a cube? Turning it around the body diagonal HB by 120° would not change anything: It looks the same as before. If you connect the battery to the points H and B, on the same axes, nothing happens again as the battery transforms into itself.
In the other case, the battery is in the mirror plane EHCB. The point A is mirror image of F, and D, G are also mirror images to each other, so they are equivalent.

ehild
 

Attachments

  • symmetry.JPG
    symmetry.JPG
    9.5 KB · Views: 493
Thank you ! So much respect .
 
Just a little more help . Please explain what's up with this one
1rjNe.png

Where is the symmetry here if the Cell is connected btw A and B ?
Also in the second figure why doesn't current flow through FG and AD ?
 
Last edited:
It is a mirror plane again...

ehild
 

Attachments

  • sym2.JPG
    sym2.JPG
    4.4 KB · Views: 438

Similar threads

Potential difference between two points in an electric field
  • · Replies 1 ·
Replies
1
Views
2K
Finding potential at a point in capacitor
  • · Replies 2 ·
Replies
2
Views
2K
How to determine if electrical components are connected in parallel or in series?
  • · Replies 10 ·
Replies
10
Views
1K
Electric potential due to shell containing a charge at an offset outside
  • · Replies 5 ·
Replies
5
Views
1K
What is the potential at point D in the circuit
  • · Replies 9 ·
Replies
9
Views
2K
Determine the Electrical potential at a given point
  • · Replies 7 ·
Replies
7
Views
2K
Minimizing the Energy of Two Conductors Very Far Apart
  • · Replies 23 ·
Replies
23
Views
2K
Electric potential at an unknown point
  • · Replies 2 ·
Replies
2
Views
1K
Calculating eletric potential using line integral of electric field
  • · Replies 1 ·
Replies
1
Views
2K
Potential difference between two points in a loop
  • · Replies 14 ·
Replies
14
Views
3K