- #1
brenfox
- 71
- 1
Homework Statement
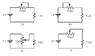
A circuit shows a 10kΩ Pot with a 5k Ω load. Determine the position of the slider on the pot when the voltage across the 5kΩ load is 3 volts. The input voltage is 9 volts.
Homework Equations
The Attempt at a Solution
Input voltage = 9 volts. Output voltage = 3 volts. Therefore the ratio of the resistance must be 3/9. Which equates to 1/3. So 10Ω/3 = 3.3Ω is the position of the Pot.Am i on the right track? Any help would be appreciated.